MitRes

A typical process for running experiments on quantum devices is as follows: first a logical quantum circuit is constructed, next it is compiled to fit to the constraints of the quantum device of choice (such as the connectivity graph or set of gate primitives) before being sent to the device via the hardware manufacturers language of choice. Finally results are returned, typically as a sequence of Shots, each shot being a single set of bit corresponding to the measurement result of each qubit.

In its basic capacity the MitRes.run method will run each of these tasks sequentially.

from qermit import MitRes, CircuitShots
from pytket import Circuit
from pytket.extensions.qiskit import AerBackend

mitres = MitRes(backend = AerBackend())
c = Circuit(2,2).H(0).Rz(0.25,0).CX(1,0).measure_all()
results = mitres.run([CircuitShots(Circuit = c, Shots = 50)])
print(results[0].get_counts())

Counter({(0, 0): 25, (1, 0): 25})

In the above code snippet a Bell circuit is simulated on the AerBackend, returning a pytket BackendResult object.

The MitRes object holds a graph of MitTask (or TaskGraph, see later clarification) objects (a TaskGraph). A MitTask object is a pure function that computes some basic step in a typical experiment. When the run function is called, a topological sort is applied to the graph to order these tasks. Each is then run sequentially.

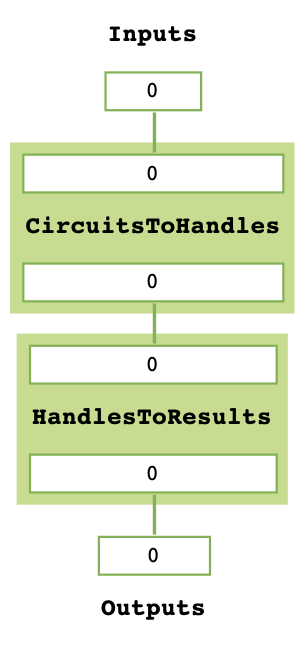
The MitTask objects held in a MitRes can be visualised with the MitRes.get_task_graph method.

mitres.get_task_graph()

It is also possible to import and use the MitTask objects directly.

from qermit.taskgraph import backend_handle_task_gen, backend_res_task_gen

sim_backend = AerBackend()
circuits_to_handles_task = backend_handle_task_gen(sim_backend)
handles_to_results_task = backend_res_task_gen(sim_backend)

print(circuits_to_handles_task)
print(handles_to_results_task)


handles = circuits_to_handles_task(([CircuitShots(Circuit = c, Shots = 50)],))
results = handles_to_results_task(handles)
print(results[0][0].get_counts())

<MitTask::CircuitsToHandles>
<MitTask::HandlesToResults>
Counter({(1, 0): 30, (0, 0): 20})

You may notice that the arguments of the MitTask objects are different, requiring Tuple type objects. This is necessary for the execution in the TaskGraph.run method. All typing information is accessible via the qermit documentation.

Error-mitigation with MitRes

To produce a MitRes object that executes an error-mitigation protocol when the MitRes.run method is called, additional MitTask objects need to be added to its task graph.

The defining characteristic of a MitRes object is that the first MitTask object in its sorted graph requires a List[CircuitShots] object as its sole argument and that the final MitTask object in its sorted graph returns a List[BackendResult] object. This is a crucial type constraint required for the combining of error-mitigation methods.

Given this, there are two viable approaches to producing error-mitigation MitRes objects, either extending a MitRes object with new MitTask objects under strict type constraints, or constructing a TaskGraph object with relaxed type constraints on internal tasks and then casting to a MitRes object at completion.

Extending MitRes with MitTask

We have already seen that the basic construction of a MitRes object has two MitTask objects, one submitting Circuit to a pytket Backend to retrieve unique handles, the other submitting these handles back to the Backend to retrieve BackendResult.

The MitRes.append and MitRes.prepend methods can be used to extend the MitTask objects the MitRes._task_graph attribute holds.

As an example, Let’s construct a basic MitRes object and then prepend a task that compiles circuits. While a common task in any experiment workflow, the basic MitRes constructor does not add a MitTask for compilation. This is because error-mitigation methods often produce circuits with very specific structures that need to be retained. Even basic compilation may destroy these structures.

from qermit import MitTask

A MitTask object is defined by four attributes: a name, a function it computes, the number of arguments to said function and the number of elements in a Tuple it returns.

Let’s define a basic function that compiles Circuits to a given Backend.

from pytket import Circuit
from pytket.backends import Backend
from typing import List

def compile_circuits(backend: Backend, circuits: List[Circuit]) -> List[Circuit]:
   for c in circuits:
      backend.compile_circuit(c)
   return circuits

This is a straightforward function definition for those familiar with pytket and completes our goal. However, this will require some minor modification before we can add it to our MitRes object.

We have already noted that a MitRes object is defined by the property that the MitRes.run method takes a List[CircuitShots] as an argument and returns a List[BackendResult]. Considering this, the MitRes.append and MitRes.prepend methods have restrictions on what MitTask objects they can add to a task graph.

The MitRes.append method can only append tasks that have one out wire and return Tuple[List[BackendResult]] from the internal method, while the MitRes.prepend method can only prepend tasks that have one in wire and expects a single argument of type List[CircuitShots] to its internal method. The Tuple type is necessary for piping data through the internal graph.

Let’s rework the compile_circuits method to fit the List[CircuitShots] constraint.

from qermit import CircuitShots
from typing import Tuple

def compile_circuit_shots(backend: Backend, circuit_shots: List[CircuitShots]) -> Tuple[List[CircuitShots]]:
  compiled_circuit_shots = []
  for cs in circuit_shots:
        compiled_circuit = backend.get_compiled_circuit(cs.Circuit)
        compiled_circuit_shots.append((compiled_circuit, cs.Shots))
  return (compiled_circuit_shots,)

Notice that MitRes.prepend does not allow tasks that pass Backend objects as arguments. When the MitRes class constructor is called with a given Backend, this same Backend is used to construct <MitTask::CircuitsToHandles> and <MitTask::HandlesToResults> objects via MitTask generator functions. In this way each method references the same Backend object, meaning it can be used to store and pass basic information such as device characteristics.

Let’s work the compile_circuit_shots method here into a similar generator function for a MitTask object.

def backend_compile_circuit_shots_task_gen(
   backend: Backend
   ) -> MitTask:
   def compile_circuit_shots(obj, circuit_shots: List[CircuitShots]) -> Tuple[List[CircuitShots]]:
      compiled_circuit_shots = []
      for cs in circuit_shots:
            compiled_circuit = backend.get_compiled_circuit(cs.Circuit)
            compiled_circuit_shots.append((compiled_circuit, cs.Shots))
      return (compiled_circuit_shots,)

   return MitTask(
      _label="CompileCircuitShots", _n_in_wires=1, _n_out_wires=1, _method=compile_circuit_shots
   )

When called, backend_compile_circuit_shots_task_gen will return a MitTask object with a callable that compiles a List[CircuitShots] to the defined backend.

from pytket.extensions.qiskit import AerBackend

sim_backend = AerBackend()
mit_task = backend_compile_circuit_shots_task_gen(sim_backend)
print(mit_task)

<MitTask::CompileCircuitShots>

The callable expects a Tuple of the arguments to the MitTask._method attribute.

test_circuit_shots = [CircuitShots(Circuit = Circuit(2).CZ(0,1).measure_all(), Shots = 10)]
test_results = mit_task((test_circuit_shots,))
print(test_results)

([CircuitShots(Circuit=[TK1(0.5, 0.5, 0.5) q[1]; CX q[0], q[1]; Measure q[0] --> c[0]; TK1(0.5, 0.5, 0.5) q[1]; Measure q[1] --> c[1]; ], Shots=10)],)

We can see that the circuit has been compiled to the AerBackend gate set primitive and returned a suitable type - Let’s prepend it to the basic MitRes object.

mit_res = MitRes(sim_backend)
mit_res.prepend(mit_task)
mit_res.get_task_graph()

If we were to use the MitRes.run method now to run an experiment, all circuits would be compiled with sim_backend before being executed on the hardware. The MitRes.append method works similarly - later examples will show it in use.

Constructing MitRes from TaskGraph

Error-mitigation methods can involve complicated sequences of tasks to work. The strict type requirements of the MitRes prepend and append rules preserve properties required for combining error-mitigation methods, but restrict the possible structure and order of tasks.

If a more complicated structure of tasks is required to perform the mitigation, a MitRes object can be cast as a TaskGraph object without the same restrictions. If the final object after construction respects the MitRes type constraints then it can be cast back as a MitRes object later.

from qermit import TaskGraph

sim_backend = AerBackend()
task_graph = TaskGraph().from_TaskGraph(MitRes(sim_backend))
task_graph.get_task_graph()

Additionally to the relaxed type constraints of TaskGraph.prepend and TaskGraph.append in relation to MitRes, the TaskGraph class has additional construction methods: TaskGraph.add_n_wires and TaskGraph.parallel.

task_graph.add_n_wires(2)
task_graph.get_task_graph()

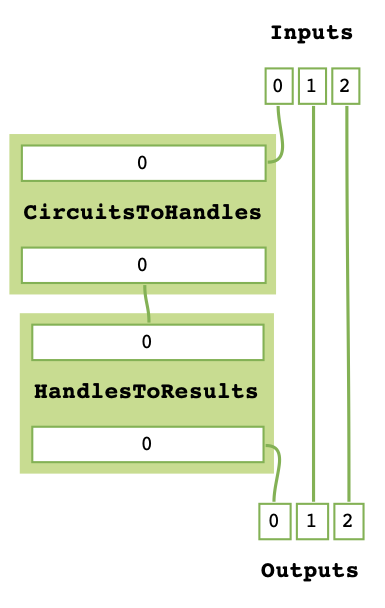
The TaskGraph.add_n_wires method adds n new edges between the input and output vertices. Similarly, the TaskGraph.parallel method adds a new path between the input and output vertices, but with a MitTask or TaskGraph object (or child) inserted.

We can add another MitRes object in parallel:

task_graph.parallel(MitRes(sim_backend))
task_graph.get_task_graph()

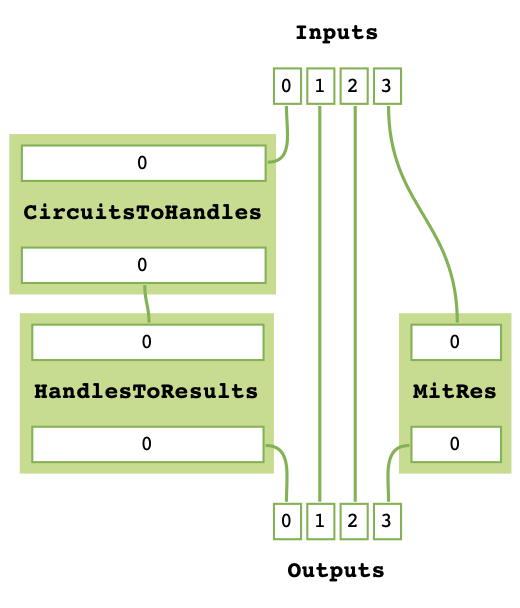
The MitRes object is added to the graph as its own callable. The MitRes.decompose_TaskGraph_nodes method will recursively substitute any graph node with a _task_graph attribute with said _task_graph, adding unique names to aid understanding.

task_graph.decompose_TaskGraph_nodes()
task_graph.get_task_graph()

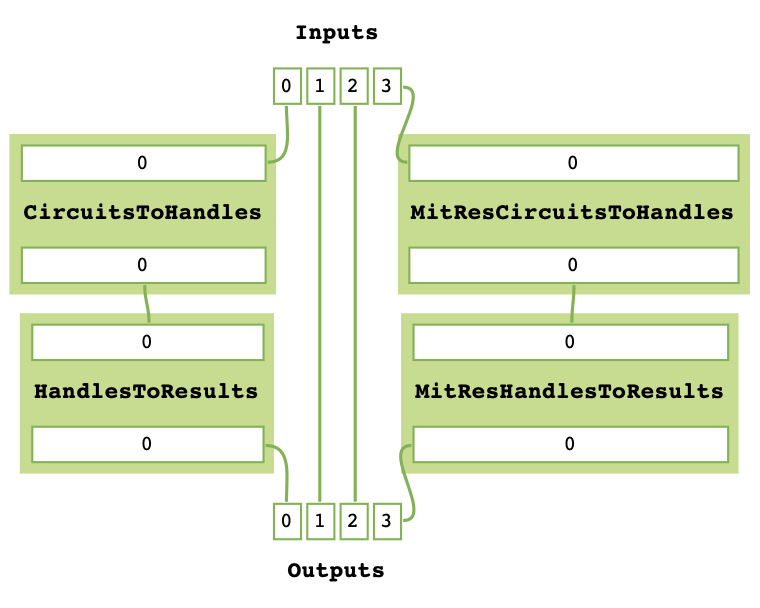
Any MitTask object we want to pass to TaskGraph.prepend must have four output wires and any number of input wires, while any MitTask object we want to pass to TaskGraph.append must have four input wires and any number of output wires. Every wire must have a type defined Wire.

Furthermore, each MitTask would also be expected to match the types of the edges being added to them, though TaskGraph only checks this during TaskGraph.run and not at graph construction as with MitRes and MitEx.

from qermit.taskgraph import Wire

def prepend_task_gen() -> MitTask:
   def task(obj, wire0: Wire, wire1: Wire) -> Tuple[List[CircuitShots], Wire, Wire, List[CircuitShots]]:
      c0 = Circuit(3).X(0).measure_all()
      c1 = Circuit(3).X(2).CX(2,0).X(2).measure_all()
      return ([CircuitShots(Circuit=c0, Shots=15)], wire0, wire1, [CircuitShots(Circuit=c1, Shots=10)])
   return MitTask(
      _label="PrependTask", _n_in_wires=2, _n_out_wires=4, _method=task
   )

prepend_task = prepend_task_gen()
print(prepend_task)
for r in prepend_task(("nO nietsniE", "hcaeB ehT")):
   print(r)

<MitTask::PrependTask>
[CircuitShots(Circuit=[Measure q[1] --> c[1]; Measure q[2] --> c[2]; X q[0]; Measure q[0] --> c[0]; ], Shots=15)]
nO nietsniE
hcaeB ehT
[CircuitShots(Circuit=[Measure q[1] --> c[1]; X q[2]; CX q[2], q[0]; Measure q[0] --> c[0]; X q[2]; Measure q[2] --> c[2]; ], Shots=10)]
We can add this ``MitTask`` to our ``TaskGraph`` object.

task_graph.prepend(prepend_task)
task_graph.get_task_graph()

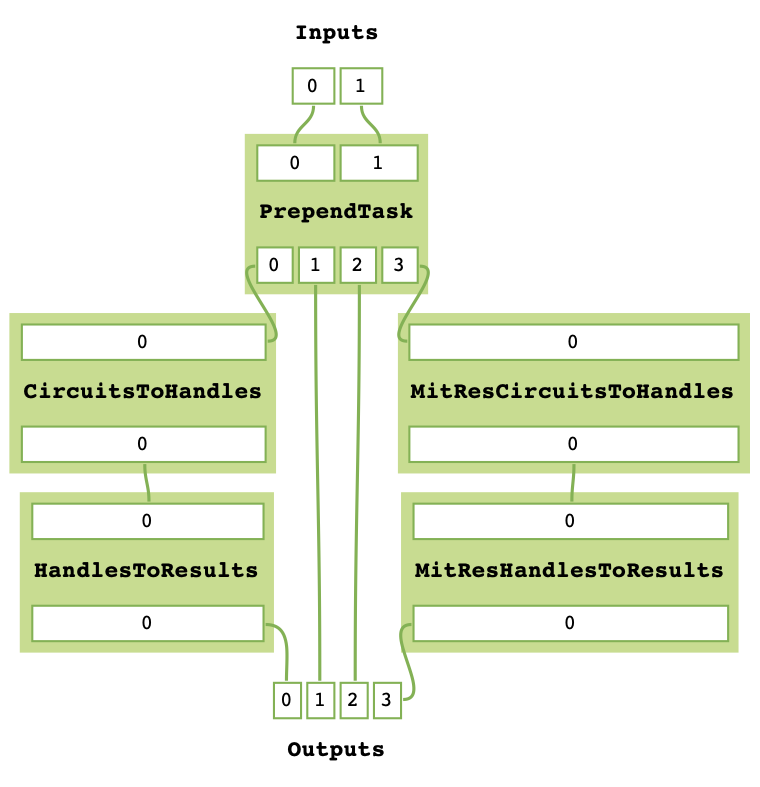
We can construct a similar MitTask for TaskGraph.append.

from functools import reduce
import operator
from typing import Counter
from pytket.backends.backendresult import BackendResult


def append_task_gen() -> MitTask:
   def task(obj, results0: List[BackendResult], wire0: Wire, wire1: Wire, results1: List[BackendResult]) -> Tuple[Wire, Counter]:
       both_counts = [results0[0].get_counts(), results1[0].get_counts()]
       combined_counts = reduce(operator.add, both_counts)
       return (wire0[::-1] + " " + wire1[::-1], combined_counts)
   return MitTask(
      _label="AppendTask", _n_in_wires=4, _n_out_wires=2, _method=task
   )

task_graph.append(append_task_gen())
task_graph.get_task_graph()
print(task_graph.run(("nO nietsniE", "hcaeB ehT")))

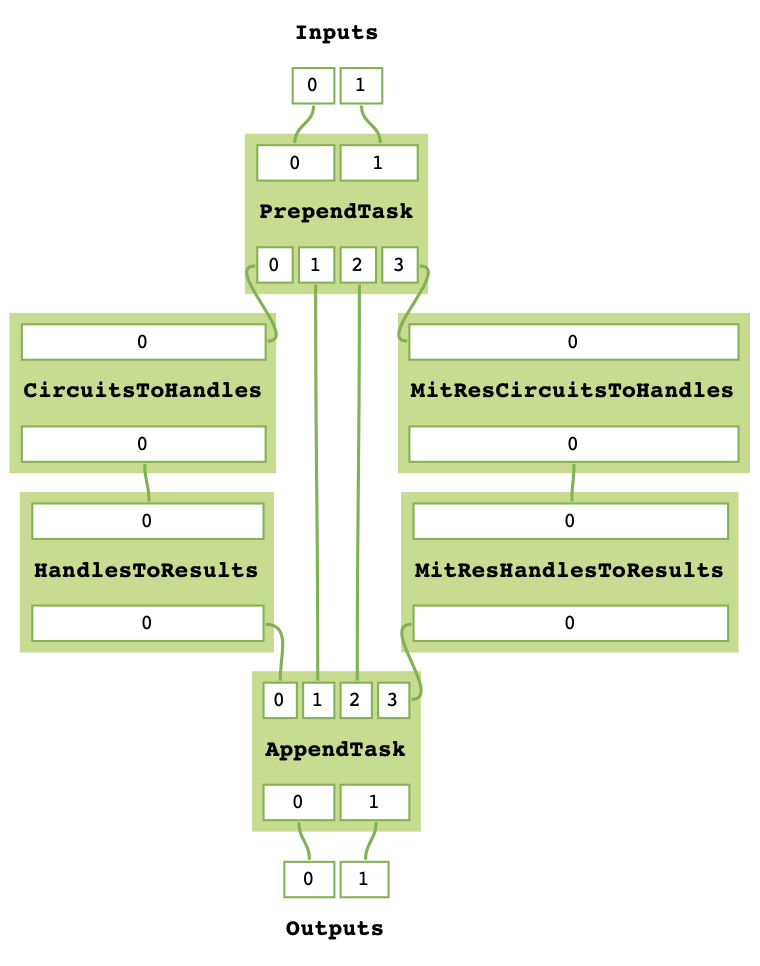
('Einstein On The Beach', Counter({(1, 0, 0): 25}))

While this example is nonsensical in regards to actual, useful, experiments, it displays how more useful structures of TaskGraph can be produced.

In its current format however, we can not cast this TaskGraph object as a MitRes.

MitRes(sim_backend).from_TaskGraph(task_graph)

TypeError: Type signature of passed task_graph.run method does not equal MitRun.run type signature. Number of in and out wires does not match.

To produce a MitRes object from this TaskGraph we need to append and prepend MitTask in such a way that the MitRes type constraints are respected.

from pytket.utils.outcomearray import OutcomeArray

def type_constraint_prepend_task_gen() -> MitTask:
      def task(obj, cs: List[CircuitShots]) -> Tuple[Wire, Wire]:
         return ("nO nietsniE", "hcaeB ehT")
      return MitTask(
         _label="TypePrependTask", _n_in_wires=1, _n_out_wires=2, _method=task
      )

def type_constraint_append_task_gen() -> MitTask:
      def task(obj, anything_comb: Wire, counter: Counter) -> Tuple[List[BackendResult]]:
         counter = Counter(
               {
                  OutcomeArray.from_readouts([key]): val
                  for key, val in counter.items()
               }
         )
         return([BackendResult(counts = counter)],)
      return MitTask(
         _label="TypeAppendTask", _n_in_wires=2, _n_out_wires=1, _method=task
      )

task_graph.prepend(type_constraint_prepend_task_gen())
task_graph.append(type_constraint_append_task_gen())

cast_mitres = MitRes(sim_backend).from_TaskGraph(task_graph)

cast_mitres.get_task_graph()

print(cast_mitres.run(([],)))

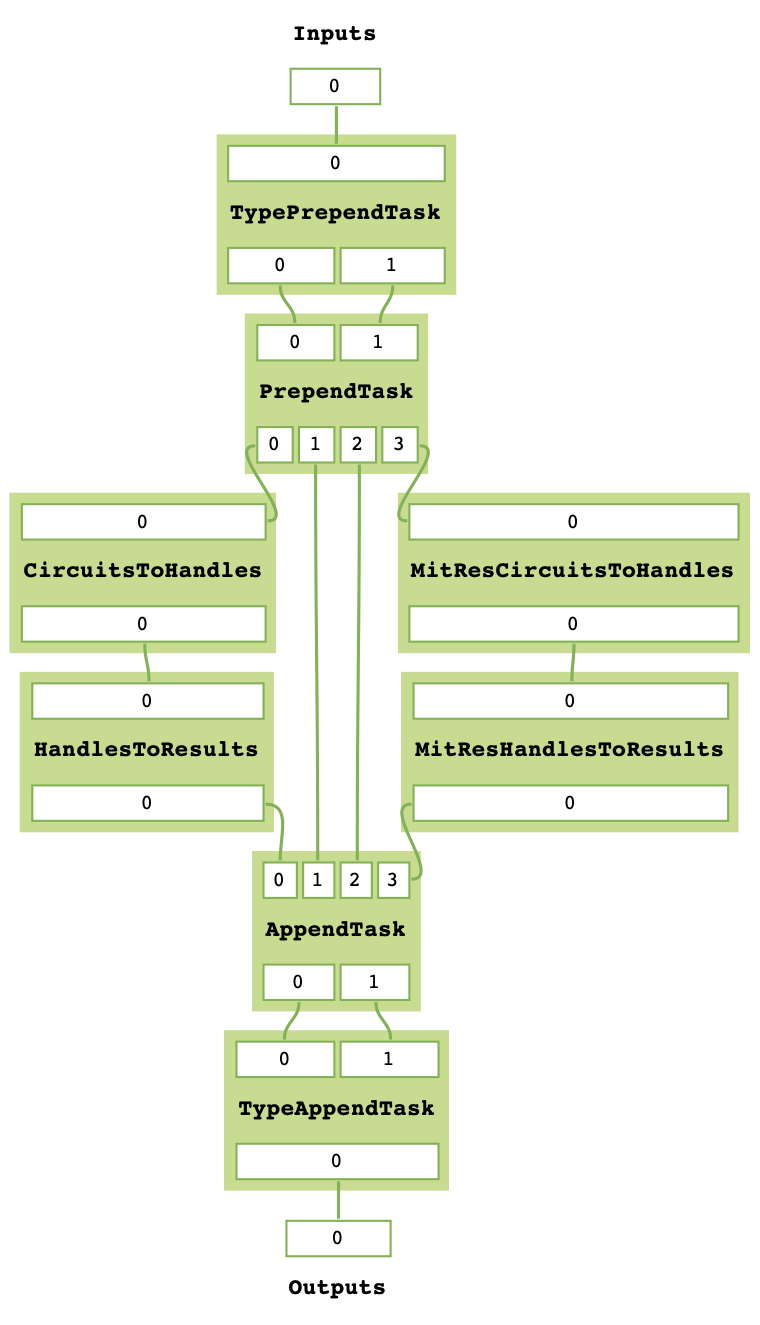
[BackendResult(q_bits={},c_bits={c[0]: 0, c[1]: 1, c[2]: 2},counts=Counter({OutcomeArray([[128]], dtype=uint8): 25}),shots=None,state=None,unitary=None,density_matrix=None)]

With this illustrative introduction to constructing advanced TaskGraph objects complete, Let’s move on to actual error-mitigation techniques available in qermit.

There are two MitRes error-mitigation methods available in qermit; SPAM correction and Frame Randomisation. Error-mitigation methods are available via a selection of generator functions. When called, the error-mitigation method of choice is constructed by acting on a MitRes object with the construction methods just discussed. In this manner composition is facilitated, as each generator method allows the error-mitigation method to be constructed around custom MitRes objects using keyword arguments.

SPAM Mitigation in qermit

A prominent source of noise is that occurring during State Preparation and Measurement (SPAM).

SPAM error-mitigation methods can correct for such noise through a post-processing step that modifies the output distribution measured from repeatedly sampling shots. This is possible given the assumption that SPAM noise is not dependent on the quantum computation run.

By repeatedly preparing and measuring a basis state, a distribution over basis states is procured. While for a perfect device the distribution would be the prepared basis state with probability 1, for devices prone to SPAM noise this distribution is perturbed and other basis states may be returned with (expected) small probability.

If this process is repeated for all (or a suitable subset given many qubits won’t experience correlated SPAM errors) basis states, a transition matrix can be derived that describes the noisy SPAM process. Simply applying the inverse of this transition matrix to the distribution of a quantum state from some desired quantum computation can effectively uncompute the errors caused by SPAM noise.

Generators for SPAM MitRes objects are available in the qermit.spam SPAM module.

from qermit.spam import gen_UnCorrelated_SPAM_MitRes
from pytket.extensions.qiskit import IBMQEmulatorBackend

lagos_backend = IBMQEmulatorBackend(
   "ibm_lagos",
   hub='',
   group='',
   project='',
)
uc_spam_mitres = gen_UnCorrelated_SPAM_MitRes(
   backend = lagos_backend,
   calibration_shots = 500
)
uc_spam_mitres.get_task_graph()

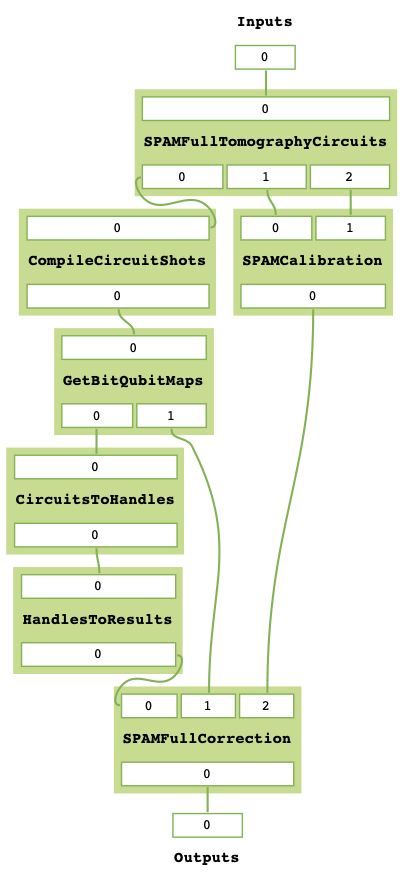
The gen_UnCorrelated_SPAM_MitRes generator function returns a MitRes object for performing SPAM mitigation with the assumption that readout errors are not correlated between qubits. As in practice this is not always the case, another generator function gen_FullyCorrelated_SPAM_MitRes allows correlations to be specified using Node from the Backend.device attribute.

from qermit.spam import gen_FullyCorrelated_SPAM_MitRes

lagos_nodes = lagos_backend.backend_info.architecture.nodes
correlated_nodes = [lagos_nodes[:3], lagos_nodes[3:]]
spam_mitres_fc = gen_FullyCorrelated_SPAM_MitRes(backend = lagos_backend,
                                                   correlations = correlated_nodes,
                                                   calibration_shots = 500)

The correlation keyword argument expects a List[List[Node]] object, where each sub-list specifies correlated device qubits. The method will raise an error if a qubit is multiple sub-list.

The uc_spam_mitres object can run experiments like any other MitRes. Let’s run an experiment both with and without both error-mitigation and none to compare usage and results.

from qermit.taskgraph import gen_compiled_MitRes

compile_mitres = gen_compiled_MitRes(backend = lagos_backend)
compile_mitres.get_task_graph()

The gen_compiled_MitRes generator function returns a MitRes object with a compilation task prepended, as with the MitRes we constructed earlier.

from pytket import Circuit
from qermit import CircuitShots

test_c_0 = Circuit(4).X(0).X(2).measure_all()
test_c_1 = Circuit(4).X(1).X(3).measure_all()

test_experiment = [CircuitShots(Circuit = test_c_0, Shots = 1000), CircuitShots(Circuit = test_c_1, Shots = 1000)]
basic_results = compile_mitres.run(test_experiment)

print(basic_results[0].get_counts())
print(basic_results[1].get_counts())

Counter({(1, 0, 1, 0): 916, (1, 1, 1, 0): 31, (0, 0, 1, 0): 21, (1, 0, 0, 0): 18, (1, 0, 1, 1): 13, (0, 1, 1, 0): 1})
Counter({(0, 1, 0, 1): 910, (0, 0, 0, 1): 54, (0, 1, 0, 0): 17, (0, 1, 1, 1): 12, (1, 1, 0, 1): 4, (0, 0, 0, 0): 3})

While the circuits constructed should have deterministic outputs, (1, 0, 1, 0) and (0, 1, 0, 1) respectively, we can see that the counts are returning some shots for other basis states. The lagos_backend used for these examples is a simulator Backend run with a noise model to emulate the properties of the Lagos device available through IBMQ, including readout errors.

spam_mitigated_results = uc_spam_mitres.run(test_experiment)
print(spam_mitigated_results[0].get_counts())
print(spam_mitigated_results[1].get_counts())

Counter({(1, 0, 1, 0): 981, (1, 0, 1, 1): 15, (1, 1, 1, 1): 2, (0, 0, 0, 0): 1, (0, 1, 0, 1): 1, (0, 1, 1, 0): 1, (1, 0, 0, 1): 1, (1, 1, 0, 0): 1})
Counter({(0, 1, 0, 1): 992, (1, 1, 0, 1): 7, (0, 1, 1, 1): 2, (0, 0, 0, 0): 1, (0, 0, 1, 0): 1, (1, 0, 0, 0): 1, (1, 0, 1, 1): 1, (1, 1, 1, 0): 1})

The device SPAM characterisation produced is stored inside the characterisation attribute the MitRes object. If a characterisation is already available for a given method when MitRes.run is called, then it will not be characterised again. This characterisation can be accessed by calling MitRes.get_characterisation().

Naively comparing counts, we can see that by using the MitRes object returned by gen_UnCorrelated_SPAM_MitRes a greater proportion of the returned shots are the deterministic outputs we expected. We can not make any grand peformance claims based off this example alone, but we can see how SPAM error-mitigation can improve results. However as emphasised earlier, MitRes objects can work with any pytket Backend object, meaning we can easily run this experiment again using the real IBMQ Lagos device simply by switching the Backend object passed to the generator function.

Also note that there is some statistical noise and the returned set of counts for SPAM error-mitigation has slightly more counts than specified. This is an artifact of the correction procedure, but importantly we can see that the returned distribution is closer to the ideal.

from pytket.extensions.qiskit import IBMQBackend

lagos_real = IBMQBackend(
   "ibm_lagos",
   hub='',
   group='',
   project='',
)
compile_mitres_real = gen_compiled_MitRes(backend = lagos_real)
uc_spam_mitres_real = gen_UnCorrelated_SPAM_MitRes(backend = lagos_real, calibration_shots = 500)

basic_results_real = compile_mitres_real.run(test_experiment)
spam_mitigated_results_real = uc_spam_mitres_real.run(test_experiment)

To complete our comparison on real hardware, results from the Lagos device without SPAM error-mitigation:

print(basic_results_real[0].get_counts())
print(basic_results_real[1].get_counts())

Counter({(1, 0, 1, 0): 808, (1, 0, 0, 0): 98, (1, 1, 1, 0): 50, (0, 0, 1, 0): 22, (1, 0, 1, 1): 8, (1, 1, 0, 0): 4, (0, 0, 0, 0): 3, (1, 1, 1, 1): 3, (0, 1, 1, 0): 2, (0, 0, 1, 1): 1, (0, 1, 0, 0): 1})
Counter({(0, 1, 0, 1): 891, (0, 0, 0, 1): 60, (0, 1, 0, 0): 26, (0, 1, 1, 1): 11, (1, 1, 0, 1): 9, (0, 0, 0, 0): 2, (0, 1, 1, 0): 1})

Results from the Lagos device with SPAM error-mitigation:

print(spam_mitigated_results_real[0].get_counts())
print(spam_mitigated_results_real[1].get_counts())

Counter({(1, 0, 1, 0): 993, (0, 1, 1, 0): 4, (1, 0, 0, 0): 2, (0, 0, 0, 0): 1, (0, 0, 0, 1): 1, (0, 0, 1, 0): 1, (0, 1, 0, 0): 1, (1, 1, 0, 1): 1})
Counter({(0, 1, 0, 1): 984, (1, 1, 0, 1): 7, (0, 0, 0, 0): 4, (0, 0, 1, 1): 3, (0, 1, 1, 0): 2, (1, 0, 0, 0): 2, (1, 0, 0, 1): 1, (1, 1, 1, 0): 1})

As with the emulator Backend, the distribution of results returned with SPAM error-mitigation for this simple test case is improved.

Frame-Randomisation in qermit

While it is not possible to efficiently characterise and suppress all device noise, it can be advantageous to transform some adverse type of noise into a less damaging type.

Coherent errors are additional unwanted unitary rotations that may appear throughout a quantum computation. Their effect can be damaging due to a possible faster rate of error accumulation than in the case of probabilistic (incoherent) errors.

Randomisation protocols can be used to tailor the form of the noise profile. By averaging the n-qubit noise channel over all elements from a group (specifically some subgroup of the full unitary group on n qubits), the resulting noise is invariant under the action of any element from this group.

For example, averaging a noise channel over the n-qubit Pauli group has the effect of producing an n-qubit stochastic Pauli channel – this is a probabilistic linear combination of n-qubit Pauli unitary errors.

In this manner, an n-qubit coherent noise channel can be tailored into an n-qubit stochastic Pauli noise channel. For Pauli channels, the worst case error rate is similar to the average error rate, whilst for coherent noise the worst case error rate scales as a square root of the average error rate.

Generator functions in the qermit.frame_randomisation frame randomisation module return MitRes objects for automatically using randomised protocols when running experiments.

Randomised compilation [Wallman2015] is a well known example of such a procedure.

from qermit.frame_randomisation import gen_Frame_Randomisation_MitRes

fr_mitres = gen_Frame_Randomisation_MitRes(lagos_backend, samples = 200)

fr_mitres.get_task_graph()

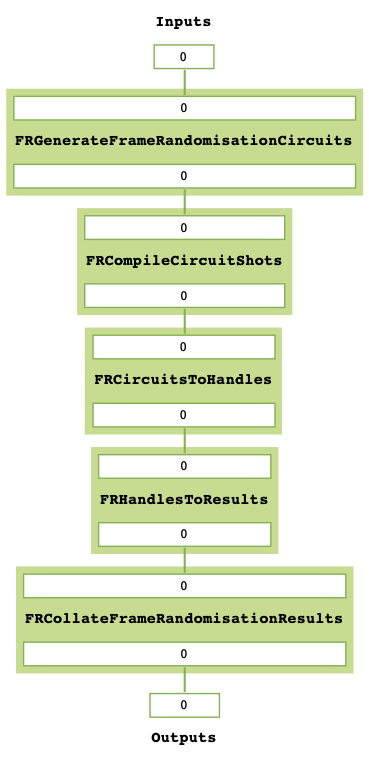
The returned MitRes object uses FrameRandomisation methods as available in the pytket.tailoring tailoring module.

The frame randomisation method used can be changed with the frame_randomisation keyword argument, which accepts methods defined in the FrameRandomisation enum class, supporting PauliFrameRandomisation and UniversalFrameRandomisation as defined in pytket. Without specification, the method will default use UniversalFrameRandomisation.

An extended explanation of these methods is available in the pytket manual.

from qermit.frame_randomisation import FrameRandomisation

pfr_mitres = gen_Frame_Randomisation_MitRes(lagos_real,
                                          samples = 200,
                                          frame_randomisation = FrameRandomisation.PauliFrameRandomisation,
                                          optimisation_level = 0)

ufr_mitres = gen_Frame_Randomisation_MitRes(lagos_real,
                                          samples = 200,
                                          frame_randomisation = FrameRandomisation.UniversalFrameRandomisation,
                                          optimisation_level = 0)

The gen_Frame_Randomisation_MitRes generator has an additional keyword argument for the optimisation_level used in the internal compilation task. For the purpose of this example we will keep this to its minimum 0, meaning that any Circuit objects will only be compiled to fit basic device constraints i.e. the gate set and fixed physical qubit connectivity.

Let’s compare performance, between a noiseless simulator, the Lagos device without any mitigation and the Lagos device with universal frame-randomisation.

from pytket.extensions.qiskit import AerBackend

test_fr_circuit = Circuit(2)
test_fr_circuit.X(0).H(1).CX(0,1).Rz(0.3, 1)
test_fr_circuit.CX(0,1).X(0).H(1).CX(0,1).Rz(0.3, 1).CX(0,1).measure_all()
test_fr_experiment = [CircuitShots(Circuit = test_fr_circuit, Shots = 3000)]

ideal_mitres = gen_compiled_MitRes(AerBackend())
ideal_res = ideal_mitres.run(test_fr_experiment)
print(ideal_res[0].get_counts())

Counter({(0, 0): 2366, (0, 1): 634})

compile_mitres_0 = gen_compiled_MitRes(lagos_real, optimisation_level = 0)
basic_results = compile_mitres_0.run(test_fr_experiment)
print(basic_results[0].get_counts())

Counter({(0, 0): 2415, (0, 1): 501, (1, 0): 63, (1, 1): 21})

ufr_results = ufr_mitres.run(test_fr_experiment)
print(ufr_results[0].get_counts())

Counter({(0, 0): 2521, (1, 0): 616, (0, 1): 52, (1, 1): 11})

pfr_results = pfr_mitres.run(test_fr_experiment)
print(pfr_results[0].get_counts())

Counter({(0, 0): 2490, (1, 0): 634, (0, 1): 59, (1, 1): 17})

Universal and Pauli Frame-Randomisation are expected to help suppress coherent errors that would usually build up over large circuits during their execution on some device. Considering these results, we could speculate that the results returned when using the mitigation MitRes object are closer to the ideal, but there aren’t enough shots here to say anything conclusive.

However, we have shown that it is as straightforward to execute any Circuit with frame-randomisation as it is without, or as it was with SPAM error-mitigation.

Combining MitRes methods

One of the key features of qermit is how it easily facilitates running combinations of error-mitigation protocols. While each error-mitigated MitRes generator will have different options for what combinations can be done, for this example we will consider combining the frame-randomisation and SPAM mitigation methods we’ve previously looked at.

As we have seen, when a generator function for a mitigated MitRes method is called, it builds the desired mitigation scheme by passing various combinations of MitTask to ``TaskGraph construction methods. In both the SPAM and frame-randomisation MitRes generators, the starting building block is a basic MitRes object - combining mitigation methods is possible by simply starting this construction from a mitigated MitRes object.

The gen_UnCorrelated_SPAM_MitRes generator has two keywords for achieving this, calibration_mitres and correction_mitres. The calibration_mitres keyword corresponds to the MitRes object through which characteriastion circuits are executed on the backend for characterisating SPAM errors, the correction_mitres keyword corresponds to the MitRes object through which experiment circuits are run (i.e. those passed to the MitRes.run method).

To show this, Let’s create a SPAM mitigation MitRes object that also runs frame-randomisation on experiment circuits.

ufr_mitres = gen_Frame_Randomisation_MitRes(lagos_real,
                                            samples = 400)

ufr_spam_mitres = gen_UnCorrelated_SPAM_MitRes(lagos_real,
calibration_shots = 500,
correction_mitres = ufr_mitres)

ufr_spam_mitres.decompose_TaskGraph_nodes()
ufr_spam_mitres.get_task_graph()

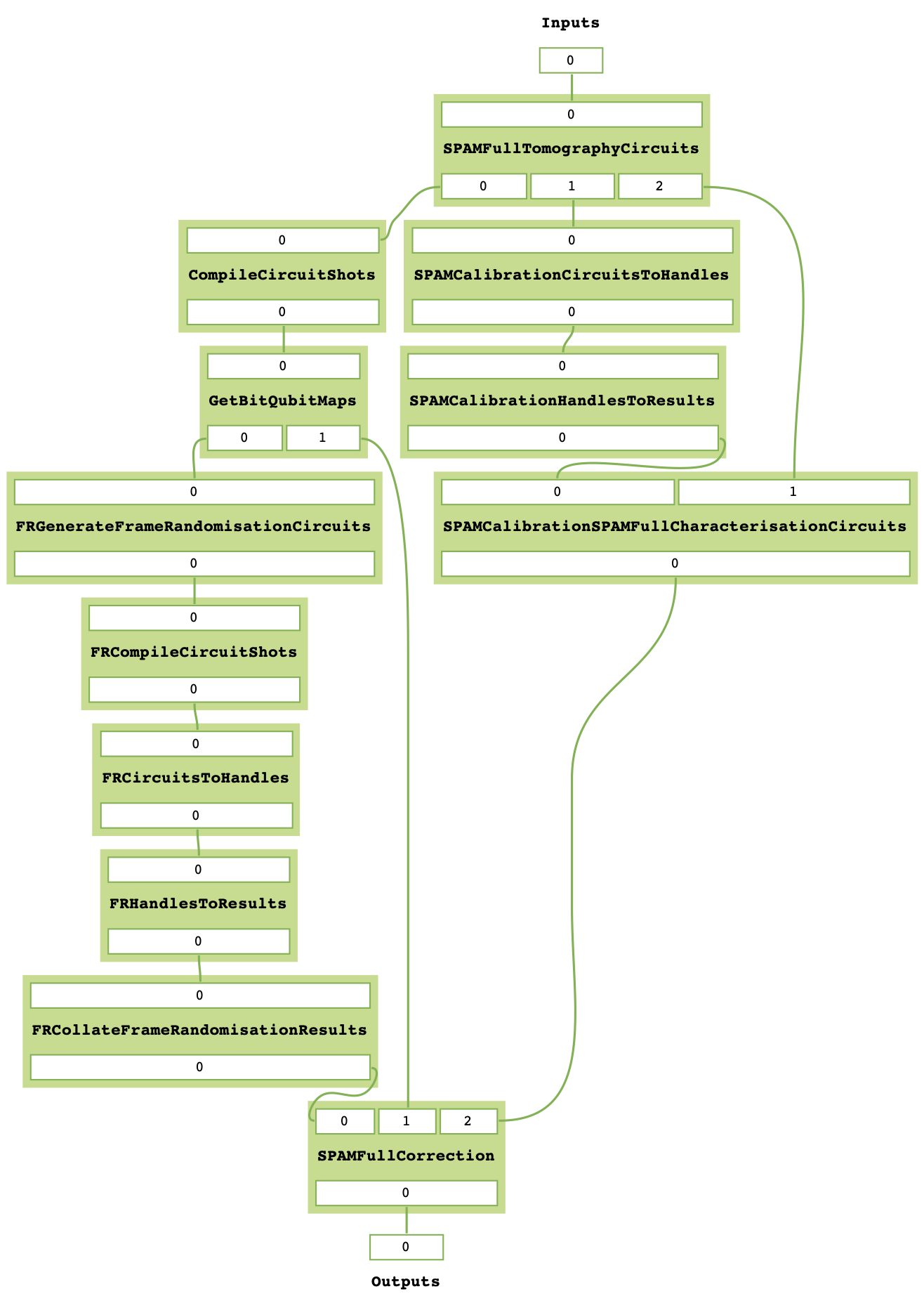
Let’s compare this task graph to the SPAM and frame-randomisation task graphs:

Comparing both images, we can see that where the default SPAM MitRes has a subgraph with a <MitTask::CircuitsToHandles> followed by a <MitTask::HandlesToResults>, the combined MitRes here has this subgraph subsituted with the frame-randomisation MitRes.

Running experiments with this combined MitRes is identical to any other MitRes.

ufr_spam_res = ufr_spam_mitres.run(test_fr_experiment)
print(ufr_spam_res[0].get_counts())

Counter({(0, 0): 2526, (1, 0): 614, (0, 1): 41, (1, 1): 21})

[Wallman2015]

Wallman, J., Emerson, J., 2015. Noise tailoring for scalable quantum computation via randomized compiling. Phys. Rev. A 94, 052325 (2016).