Training: Classical case¶
In this section, we present a complete use case of lambeq’s training module, implementing a classical pipeline on the meaning classification dataset introduced in [LPM+23]. The goal is to classify simple sentences (such as “skillful programmer creates software” and “chef prepares delicious meal”) into two categories, food or IT. The dataset consists of 130 sentences created using a simple context-free grammar.
We will use a SpiderAnsatz to split large tensors into chains of smaller ones. The pipeline uses PyTorch as a backend.
Preparation¶
We start with importing PyTorch and specifying some training hyperparameters.
import torch
BATCH_SIZE = 30
EPOCHS = 30
LEARNING_RATE = 3e-2
SEED = 0
Input data¶
Let’s read the data and print some example sentences.
def read_data(filename):
labels, sentences = [], []
with open(filename) as f:
for line in f:
t = float(line[0])
labels.append([t, 1-t])
sentences.append(line[1:].strip())
return labels, sentences
train_labels, train_data = read_data('../examples/datasets/mc_train_data.txt')
val_labels, val_data = read_data('../examples/datasets/mc_dev_data.txt')
test_labels, test_data = read_data('../examples/datasets/mc_test_data.txt')
import os
TESTING = int(os.environ.get('TEST_NOTEBOOKS', '0'))
if TESTING:
train_labels, train_data = train_labels[:2], train_data[:2]
val_labels, val_data = val_labels[:2], val_data[:2]
test_labels, test_data = test_labels[:2], test_data[:2]
EPOCHS = 1
train_data[:5]
['skillful man prepares sauce .',
'skillful man bakes dinner .',
'woman cooks tasty meal .',
'man prepares meal .',
'skillful woman debugs program .']
Targets are represented as 2-dimensional arrays:
train_labels[:5]
[[1.0, 0.0], [1.0, 0.0], [1.0, 0.0], [1.0, 0.0], [0.0, 1.0]]
Creating and parameterising diagrams¶
The first step is to convert sentences into string diagrams.
from lambeq import BobcatParser
parser = BobcatParser(verbose='text')
train_diagrams = parser.sentences2diagrams(train_data)
val_diagrams = parser.sentences2diagrams(val_data)
test_diagrams = parser.sentences2diagrams(test_data)
Tagging sentences.
Parsing tagged sentences.
Turning parse trees to diagrams.
Tagging sentences.
Parsing tagged sentences.
Turning parse trees to diagrams.
Tagging sentences.
Parsing tagged sentences.
Turning parse trees to diagrams.
The produced diagrams need to be parameterised by a specific ansatz. For this experiment we will use a SpiderAnsatz.
from lambeq.backend.tensor import Dim
from lambeq import AtomicType, SpiderAnsatz
ansatz = SpiderAnsatz({AtomicType.NOUN: Dim(2),
AtomicType.SENTENCE: Dim(2)})
train_circuits = [ansatz(diagram) for diagram in train_diagrams]
val_circuits = [ansatz(diagram) for diagram in val_diagrams]
test_circuits = [ansatz(diagram) for diagram in test_diagrams]
train_circuits[0].draw()
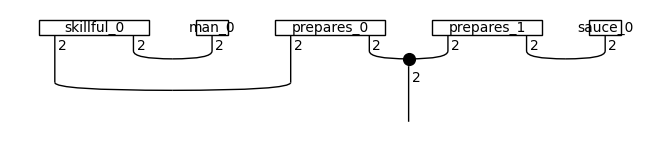
Training¶
Instantiate model¶
We can now initialise the model by importing the PytorchModel class, and passing all diagrams to the class method PytorchModel.from_diagrams().
from lambeq import PytorchModel
all_circuits = train_circuits + val_circuits + test_circuits
model = PytorchModel.from_diagrams(all_circuits)
Note
The model can also be instantiated by using the PytorchModel.from_checkpoint() method, if an existing checkpoint is available.
Additionally, the parameters can be initialised by invoking the PytorchModel.initialise_weights() method. Since Release 0.3.0, we initialise the parameters using a symmetric uniform distribution where the range is determined by the output dimension (flow codomain) of a box:
This ensures that the expected value of the L2 norm of the output of a box is approximately 1.
Define evaluation metric¶
Optionally, we can provide a dictionary of callable evaluation metrics with the signature metric(y_hat, y).
sig = torch.sigmoid
def accuracy(y_hat, y):
return torch.sum(torch.eq(torch.round(sig(y_hat)), y))/len(y)/2 # half due to double-counting
eval_metrics = {"acc": accuracy}
Initialise trainer¶
Next step is to initialise a PytorchTrainer object. Because this is a binary classification task, we will use binary cross-entropy as the loss. As an optimizer, we choose Adam with weight decay.
Note
PytorchTrainer uses PyTorch’s native classes for optimisers and losses, instead of the lambeq equivalents.
from lambeq import PytorchTrainer
trainer = PytorchTrainer(
model=model,
loss_function=torch.nn.BCEWithLogitsLoss(),
optimizer=torch.optim.AdamW,
learning_rate=LEARNING_RATE,
epochs=EPOCHS,
evaluate_functions=eval_metrics,
evaluate_on_train=True,
verbose='text',
seed=SEED)
Create datasets¶
To facilitate batching and data shuffling, lambeq provides a Dataset interface. Shuffling is enabled by default, and if not specified, the batch size is set to the length of the dataset. In our example we will use the BATCH_SIZE we have set above.
from lambeq import Dataset
train_dataset = Dataset(
train_circuits,
train_labels,
batch_size=BATCH_SIZE)
val_dataset = Dataset(val_circuits, val_labels, shuffle=False)
Train¶
Now we can pass the datasets to the fit() method of the trainer to start the training.
trainer.fit(train_dataset, val_dataset, eval_interval=1, log_interval=5)
Epoch 5: train/loss: 0.6518 valid/loss: 0.7119 train/time: 0.53s valid/time: 0.13s train/acc: 0.5643 valid/acc: 0.5500
Epoch 10: train/loss: 0.5804 valid/loss: 0.6197 train/time: 0.39s valid/time: 0.12s train/acc: 0.5714 valid/acc: 0.6167
Epoch 15: train/loss: 0.3311 valid/loss: 0.4577 train/time: 0.31s valid/time: 0.19s train/acc: 0.8643 valid/acc: 0.7667
Epoch 20: train/loss: 0.1054 valid/loss: 0.2346 train/time: 0.47s valid/time: 0.13s train/acc: 0.9500 valid/acc: 0.9333
Epoch 25: train/loss: 0.1346 valid/loss: 0.0438 train/time: 0.32s valid/time: 0.22s train/acc: 0.9857 valid/acc: 1.0000
Epoch 30: train/loss: 0.0005 valid/loss: 0.0283 train/time: 0.56s valid/time: 0.14s train/acc: 0.9929 valid/acc: 1.0000
Training completed!
train/time: 2.59s train/time_per_epoch: 0.09s train/time_per_step: 0.03s valid/time: 0.93s valid/time_per_eval: 0.03s
Note
The eval_interval controls the interval in which the model is evaluated on the validation dataset. Default is 1. If evaluation on the validation dataset is expensive, we recommend setting it to a higher value.
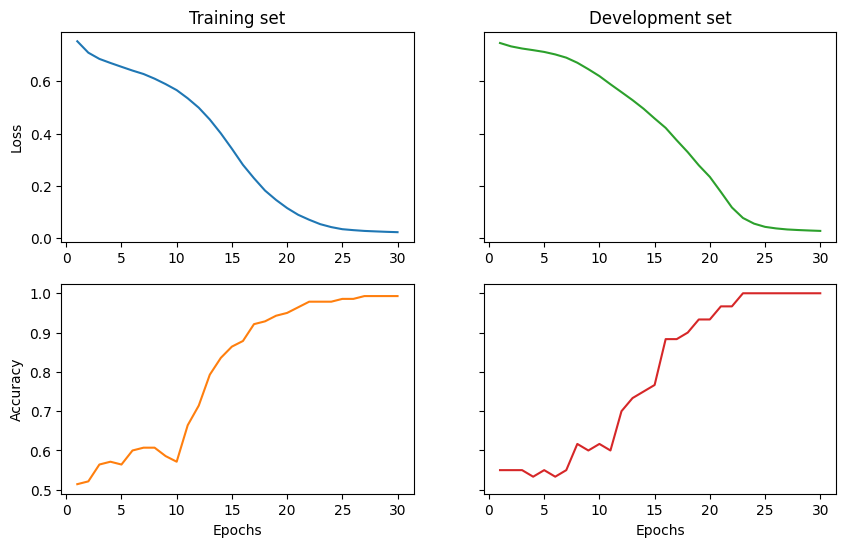
Results¶
Finally, we visualise the results and evaluate the model on the test data.
import matplotlib.pyplot as plt
import numpy as np
fig1, ((ax_tl, ax_tr), (ax_bl, ax_br)) = plt.subplots(2, 2, sharey='row', figsize=(10, 6))
ax_tl.set_title('Training set')
ax_tr.set_title('Development set')
ax_bl.set_xlabel('Epochs')
ax_br.set_xlabel('Epochs')
ax_bl.set_ylabel('Accuracy')
ax_tl.set_ylabel('Loss')
colours = iter(plt.rcParams['axes.prop_cycle'].by_key()['color'])
range_ = np.arange(1, trainer.epochs+1)
ax_tl.plot(range_, trainer.train_epoch_costs, color=next(colours))
ax_bl.plot(range_, trainer.train_eval_results['acc'], color=next(colours))
ax_tr.plot(range_, trainer.val_costs, color=next(colours))
ax_br.plot(range_, trainer.val_eval_results['acc'], color=next(colours))
# print test accuracy
test_acc = accuracy(model(test_circuits), torch.tensor(test_labels))
print('Test accuracy:', test_acc.item())
Test accuracy: 1.0
Adding custom layers to the model¶
In the default setting, the forward pass of a PytorchModel performs a simple tensor contraction of the tensorised diagrams. However, if one likes to add additional custom layers, one can create a custom model that inherits from PytorchModel and overwrite the PytorchModel.forward() method.
class MyCustomModel(PytorchModel):
def __init__(self):
super().__init__()
self.net = torch.nn.Linear(2, 2)
def forward(self, input):
"""define a custom forward pass here"""
preds = self.get_diagram_output(input)
preds = self.net(preds.float())
return preds
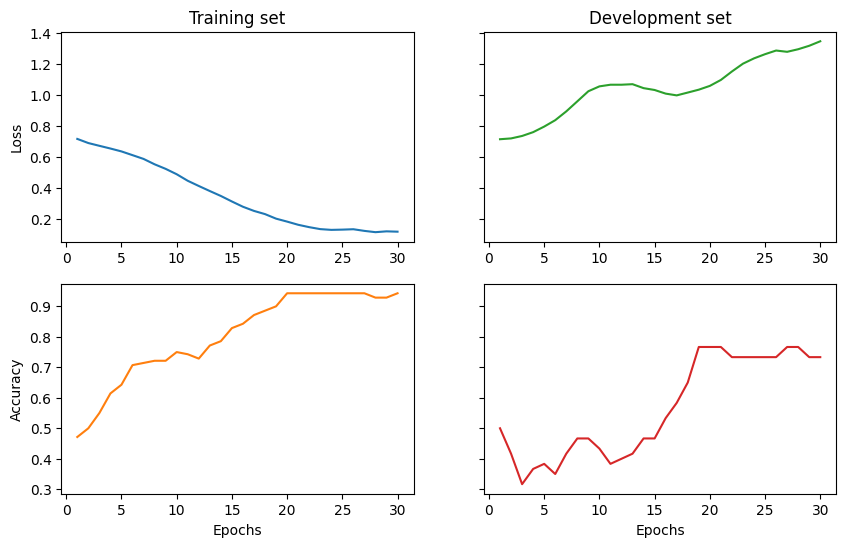
The rest follows the same procedure as explained above, i.e. initialise a trainer, fit the model and visualise the results.
custom_model = MyCustomModel.from_diagrams(all_circuits)
custom_model_trainer = PytorchTrainer(
model=custom_model,
loss_function=torch.nn.BCEWithLogitsLoss(),
optimizer=torch.optim.AdamW,
learning_rate=LEARNING_RATE,
epochs=EPOCHS,
evaluate_functions=eval_metrics,
evaluate_on_train=True,
verbose='text',
seed=SEED)
custom_model_trainer.fit(train_dataset, val_dataset, log_interval=5)
Epoch 5: train/loss: 0.6729 valid/loss: 0.7965 train/time: 0.53s valid/time: 0.13s train/acc: 0.6429 valid/acc: 0.3833
Epoch 10: train/loss: 0.4602 valid/loss: 1.0563 train/time: 0.40s valid/time: 0.13s train/acc: 0.7500 valid/acc: 0.4333
Epoch 15: train/loss: 0.4580 valid/loss: 1.0329 train/time: 0.39s valid/time: 0.19s train/acc: 0.8286 valid/acc: 0.4667
Epoch 20: train/loss: 0.1645 valid/loss: 1.0594 train/time: 0.39s valid/time: 0.13s train/acc: 0.9429 valid/acc: 0.7667
Epoch 25: train/loss: 0.1098 valid/loss: 1.2642 train/time: 0.38s valid/time: 0.12s train/acc: 0.9429 valid/acc: 0.7333
Epoch 30: train/loss: 0.1957 valid/loss: 1.3476 train/time: 0.32s valid/time: 0.19s train/acc: 0.9429 valid/acc: 0.7333
Training completed!
train/time: 2.40s train/time_per_epoch: 0.08s train/time_per_step: 0.03s valid/time: 0.89s valid/time_per_eval: 0.03s
import matplotlib.pyplot as plt
import numpy as np
fig1, ((ax_tl, ax_tr), (ax_bl, ax_br)) = plt.subplots(2, 2, sharey='row', figsize=(10, 6))
ax_tl.set_title('Training set')
ax_tr.set_title('Development set')
ax_bl.set_xlabel('Epochs')
ax_br.set_xlabel('Epochs')
ax_bl.set_ylabel('Accuracy')
ax_tl.set_ylabel('Loss')
colours = iter(plt.rcParams['axes.prop_cycle'].by_key()['color'])
range_ = np.arange(1, trainer.epochs+1)
ax_tl.plot(range_, custom_model_trainer.train_epoch_costs, color=next(colours))
ax_bl.plot(range_, custom_model_trainer.train_eval_results['acc'], color=next(colours))
ax_tr.plot(range_, custom_model_trainer.val_costs, color=next(colours))
ax_br.plot(range_, custom_model_trainer.val_eval_results['acc'], color=next(colours))
# print test accuracy
test_acc = accuracy(model(test_circuits), torch.tensor(test_labels))
print('Test accuracy:', test_acc.item())
Test accuracy: 1.0
See also: