DisCoCat in lambeq
In the previous tutorial, we learnt the basics of monoidal categories and how to represent them in lambeq. In this tutorial, we look at the Distributional Compositional Categorical model [CSC2010], which uses functors to map diagrams from the rigid category of pregroup grammars to vector space semantics.
Pregroup grammars
Pregroup grammar is a grammatical formalism devised by Joachim Lambek in 1999 [Lam1999]. In pregroups, each word is a morphism with type \(I \to T\) where \(I\) is the monoidal unit and \(T\) is a rigid type, referred to as the pregroup type. Here are some examples for pregroup type assignments:
a noun is given the base type \(n\).
an adjective consumes a noun on the noun’s left to return another noun, so it is given the type \(n\cdot n^l\).
a transitive verb consumes a noun on its left and another noun on its right to give a sentence, so is given the type \(n^r \cdot s \cdot n^l\).
In the context of pregroups, the adjoints \(n^l\) and \(n^r\) can be thought of as the left and right inverses of a type \(n\) respectively. In a pregroup derivation, the words are concatenated using the monoidal product \(\otimes\) and linked using cups, which are special morphisms that exist in any rigid category. A sentence is grammatically sound if its derivation has a single uncontracted sentence wire.
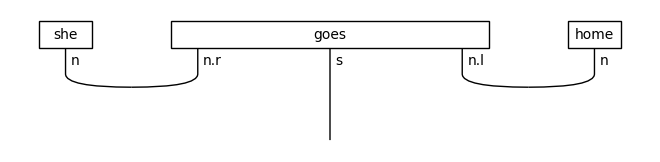
In lambeq, words are defined using the Word class. A Word is just a Box where the input type is fixed to be the monoidal unit \(I\) (or Ty()). A pregroup derivation diagram can be drawn using either the backend.grammar.Diagram.draw() method or the backend.drawing.draw() function.
[1]:
from lambeq.backend.drawing import draw
from lambeq.backend.grammar import Cap, Cup, Id, Ty, Word
n, s = Ty('n'), Ty('s')
words = [
Word('she', n),
Word('goes', n.r @ s @ n.l),
Word('home', n)
]
cups = Cup(n, n.r) @ Id(s) @ Cup(n.l, n)
assert Id().tensor(*words) == words[0] @ words[1] @ words[2]
assert Ty().tensor(*[n.r, s, n.l]) == n.r @ s @ n.l
diagram = Id().tensor(*words) >> cups
draw(diagram)
Note
In lambeq, method create_pregroup_diagram() provides an alternative, more compact way to create pregroup diagrams, by explicitly defining a list of cups and swaps. For example, the above diagram can be also generated using the following code:
from lambeq.backend.grammar import Diagram, Ty
words = [Word('she', n), Word('goes', n.r @ s @ n.l), Word('home', n)]
morphisms = [(Cup, 0, 1), (Cup, 3, 4)]
diagram = Diagram.create_pregroup_diagram(words, morphisms)
where the numbers in morphisms define the indices of the corresponding wires at the top of the diagram
(n @ n.r @ s @ n.l @ n).
[2]:
from lambeq.backend.drawing import draw_equation
# In the original diagram, words appear before the cups
print('Before normal form:', ', '.join(map(str, diagram.boxes)))
diagram_nf = diagram.normal_form()
print('After normal form:', ', '.join(map(str, diagram_nf.boxes)))
draw_equation(diagram, diagram_nf, symbol='->', figsize=(10, 4), draw_as_pregroup=False, foliated=True)
Before normal form: she, goes, home, CUP, CUP
After normal form: she, goes, CUP, home, CUP
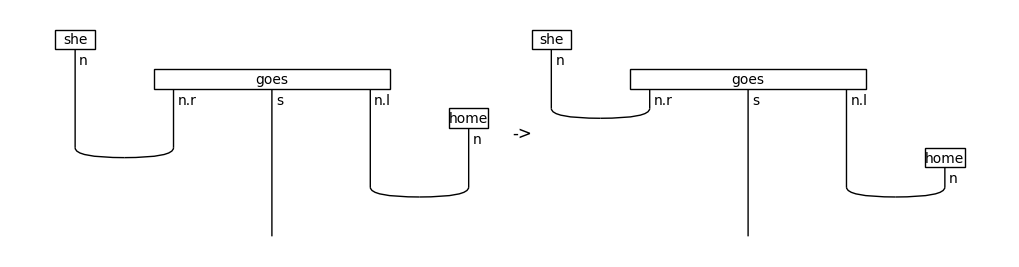
In the example above, the application of normal form to the diagram introduces a cup before the word “home”.
Functors
Given monoidal categories \(\mathcal{C}\) and \(\mathcal{D}\), a monoidal functor \(F: \mathcal{C} \to \mathcal{D}\) satisfies the following properties:
monoidal structure of objects is preserved: \(F(A \otimes B) = F(A) \otimes F(B)\)
adjoints are preserved: \(F(A^l) = F(A)^l\), \(F(A^r) = F(A)^r\)
monoidal structure of morphism is preserved: \(F(g \otimes f) = F(g) \otimes F(f)\)
compositonal structure of morphisms is preserved: \(F(g \circ f) = F(g) \circ F(f)\)
Put simply, a functor is a structure-preserving transformation. In a free monoidal category, applying a functor to a diagram amounts to simply providing a mapping for each generating object and morphism. In lambeq, a functor is defined by passing mappings (dictionaries or functions) as arguments ob and ar to the Functor class.
Functors are one of the most powerful concepts in category theory. In fact, the encoding, rewriting and parameterisation steps of lambeq’s pipeline are implemented individually as functors, resulting in an overall functorial transformation from parse trees to tensor networks and circuits. More specifically:
lambeq.CCGParseruses a functor to transform a biclosed CCG diagram to a pregroup diagram [YK2021].lambeq.Rewriterfunctorially transforms a pregroup diagram to a simpler pregroup diagram.lambeq.TensorAnsatzfunctorially transforms a pregroup diagram to a tensor diagram, which can be evaluated as a tensor network using NumPy, JAX or PyTorch.lambeq.CircuitAnsatzfunctorially transforms a pregroup diagram to a quantum circuit, for evaluation on a quantum device.
Below we present two examples of functors, implemented in lambeq.
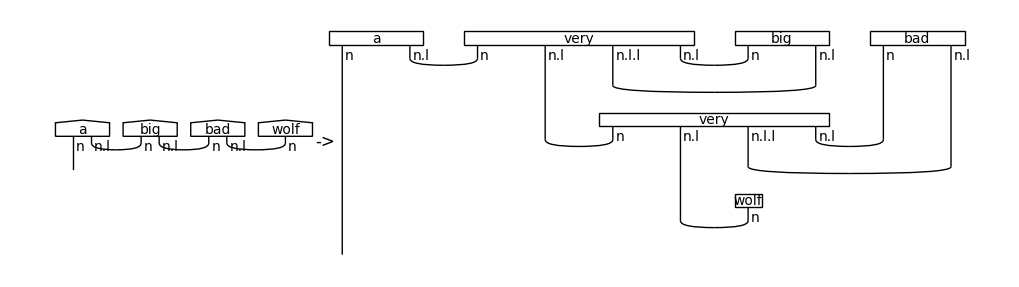
Example 1: “Very” functor
This functor adds the word “very” in front of every adjective in a DisCoCat diagram.
Since the mapping is from a grammar.Diagram to another grammar.Diagram, a grammar.Functor should be used. Further, the word “very” modifies an adjective to return another adjective, so it should have type
\((n \otimes n^l) \otimes (n \otimes n^l)^l = n \otimes n^l \otimes n^{ll} \otimes n^l\).
[3]:
from lambeq import BobcatParser
parser = BobcatParser(verbose='suppress')
[4]:
from lambeq.backend.drawing import draw_equation
from lambeq.backend.grammar import Diagram, grammar, Functor
# determiners have the same type as adjectives
# but we shouldn't add 'very' behind them
determiners = ['a', 'the', 'my', 'his', 'her', 'their']
# type for an adjective
adj = n @ n.l
very = Word('very', adj @ adj.l)
cups = Diagram.cups(adj.l, adj)
def very_ob(_, ty):
return ty
def very_ar(_, box):
if box != very:
if box.name not in determiners:
if box.cod == adj:
return very @ box >> Id(adj) @ cups
return box
very_functor = Functor(grammar,
ob=very_ob,
ar=very_ar,)
diagram = parser.sentence2diagram('a big bad wolf')
new_diagram = very_functor(diagram)
draw_equation(diagram, new_diagram, symbol='->', figsize=(10, 4))
Example 2: Twist functor
In this functor, cups and caps are treated specially and are not passed to the ar function; instead they are passed to grammar.Diagram.register_special_box() method.
Here is an example of how to map a cup to a custom diagram, such as a “twisted” cup. Note that it is up to the user to ensure the new cups and caps satisfy the snake equations.
[5]:
from lambeq.backend.grammar import Category, Ty, Layer, Diagram, Functor, Box, Cup, Cap, Swap
twisted = Category('twisted')
@twisted('Diagram')
class TwistedDiagram(Diagram): ...
@twisted('Ty')
class TwistedTy(Ty): ...
@twisted('Box')
class TwistedBox(Box): ...
@twisted('Layer')
class TwistedLayer(Layer): ...
class TwistedCup(Cup, TwistedBox): ...
class TwistedCap(Cap, TwistedBox): ...
@TwistedDiagram.register_special_box('swap')
class TwistedSwap(Swap, TwistedBox): ...
@TwistedDiagram.register_special_box('cap')
def twisted_cap_factory(left, right, is_reversed=False):
caps = TwistedCap(right, left, is_reversed=not is_reversed)
swaps = TwistedSwap(right, left)
return caps >> swaps
@TwistedDiagram.register_special_box('cup')
def twisted_cup_factory(left, right, is_reversed=False):
swaps = TwistedSwap(left, right)
cups = TwistedCup(right, left, is_reversed=not is_reversed)
return swaps >> cups
twist_functor = Functor(
ob=lambda _, ty: TwistedTy(ty.name),
ar=lambda func, box: TwistedBox(box.name, func(box.dom), func(box.cod)),
target_category=twisted)
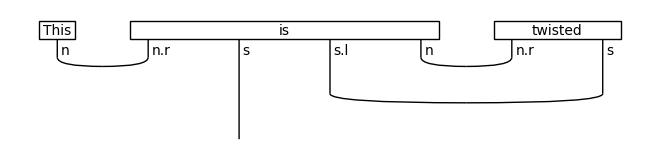
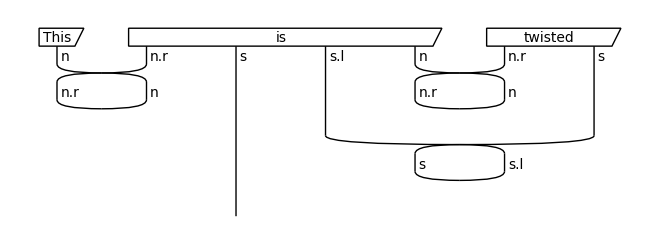
diagram = parser.sentence2diagram('This is twisted')
twisted_diagram = twist_functor(diagram)
draw(diagram)
draw(twisted_diagram)
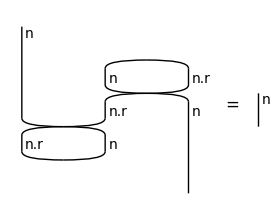
snake = Id(n) @ Cap(n.r, n) >> Cup(n, n.r).to_diagram() @ Id(n)
draw_equation(twist_functor(snake), Id(n), figsize=(4, 2))
[6]:
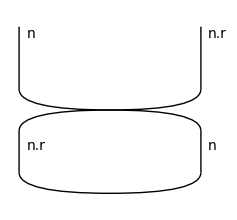
TwistedDiagram.cups(n, n.r).draw(figsize=(2, 2))
TwistedDiagram.caps(n.r, n).draw(figsize=(2, 2))
Note
Twisting the nested cups for “is” and “twisted” together is not a functorial operation, so it cannot be implemented using grammar.Functor.
Classical DisCoCat: Tensor networks
The classical version of DisCoCat sends diagrams in the category of pregroup derivations to tensors in the category of vector spaces FVect. FVect is a monoidal category with vector spaces (e.g. \(\mathbb{R}^2 \otimes \mathbb{R}^2\)) as objects and linear maps between vector spaces as morphisms. It is in fact a compact closed category, which is a special case of rigid categories where \(A^l = A^r = A^*\).
Using the lambeq.backend.tensor module, you can define a free category of vector spaces: objects are defined with the lambeq.backend.tensor.Dim class and morphisms with the lambeq.backend.tensor.Box class. Composite morphisms are constructed by freely combining the generating morphisms using the >> operator. This is similar to how rigid categories and monoidal categories are defined. The concrete value of the tensor is passed to the data attribute as an unshaped list; lambeq will reshape it later based on the input and output dimensions.
It is worth noting that lambeq.backend.tensor.Diagram delays the computation of tensor contractions until tensor.Diagram.eval() is called.
[7]:
import numpy as np
from lambeq.backend.tensor import Box, Diagram, Dim, Id
# Dim(1) is the unit object, so disappears when tensored with another Dim
print(f'{Dim(1) @ Dim(2) @ Dim(3)=}')
Dim(1) @ Dim(2) @ Dim(3)=Dim(2, 3)
[8]:
id_box = Box('Id Box', Dim(2), Dim(2), data=[1,0,0,1])
id_tensor = np.array([1, 0, 0, 1]).reshape((2, 2))
# the actual values of id_box and id_tensor are equal
assert (id_box.array == id_tensor).all()
print(f'{id_box.eval()=}')
id_box.eval()=array([[1., 0.],
[0., 1.]])
In the category of vector spaces, cups, caps and swaps take on concrete values as tensors.
[9]:
Diagram.cups(Dim(3), Dim(3)).eval(dtype=np.int64)
[9]:
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
[10]:
Diagram.swap(Dim(2), Dim(2)).eval(dtype=np.int64)
[10]:
array([[[[1, 0],
[0, 0]],
[[0, 0],
[1, 0]]],
[[[0, 1],
[0, 0]],
[[0, 0],
[0, 1]]]])
To implement a functor from grammar.Diagram to tensor.Diagram, use a grammar.Functor with target_category = lambeq.backend.tensor.tensor, and with tensor.Dim and tensor.Diagram as cod, respectively. In addition, tensor.Diagrams can be instantiated with concrete values to be evaluated later using a custom tensor contractor. See the implementation of TensorAnsatz for an example.
[11]:
import numpy as np
from lambeq.backend.grammar import Functor
from lambeq.backend import tensor
def one_ob(_, ty):
dims = [2] * len(ty)
return Dim(*dims) # does Dim(2,2,..)
def one_ar(_, box):
dom = one_ob(_, box.dom)
cod = one_ob(_, box.cod)
box = Box(box.name, dom, cod, np.ones((dom @ cod).dim))
print(f'"{box}" becomes')
print(box.data)
return box
one_functor = Functor(
target_category=tensor.tensor,
ob=one_ob, ar=one_ar,
)
one_diagram = one_functor(diagram)
print(f'{one_diagram = }')
one_diagram.draw()
"This" becomes
[1. 1.]
"is" becomes
[[[[1. 1.]
[1. 1.]]
[[1. 1.]
[1. 1.]]]
[[[1. 1.]
[1. 1.]]
[[1. 1.]
[1. 1.]]]]
"twisted" becomes
[[1. 1.]
[1. 1.]]
one_diagram = Diagram(dom=Dim(1), cod=Dim(2), layers=[Layer(left=Dim(1), box=[This; Dim(1) -> Dim(2)], right=Dim(1)), Layer(left=Dim(2), box=[is; Dim(1) -> Dim(2, 2, 2, 2)], right=Dim(1)), Layer(left=Dim(2, 2, 2, 2, 2), box=[twisted; Dim(1) -> Dim(2, 2)], right=Dim(1)), Layer(left=Dim(2, 2, 2, 2), box=[CUP; Dim(2, 2) -> Dim(1)], right=Dim(2)), Layer(left=Dim(2, 2, 2), box=[CUP; Dim(2, 2) -> Dim(1)], right=Dim(1)), Layer(left=Dim(1), box=[CUP; Dim(2, 2) -> Dim(1)], right=Dim(2))])
Quantum DisCoCat: Quantum circuits
The quantum version of DisCoCat sends diagrams in the category of pregroup derivations to circuits in the category of Hilbert spaces FHilb. This is a compact closed monoidal category with Hilbert spaces (e.g. \(\mathbb{C}^{2^n}\)) as objects and unitary maps between Hilbert spaces as morphisms.
The lambeq.backend.quantum module is a framework for the free category of quantum circuits: objects are generated using the quantum.Ty class and morphisms by using the available quantum gates which are subclasses of quantum.Box. In lambeq, rotation values range from \(0\) to \(1\) rather than from \(0\) to \(2\pi\). The circuit can then either be evaluated using tensor contraction with the eval() method, or exported to pytket using the to_tk() method, which supports multiple hardware backends.
[12]:
from lambeq.backend.quantum import CX, Id, qubit, Rz, X
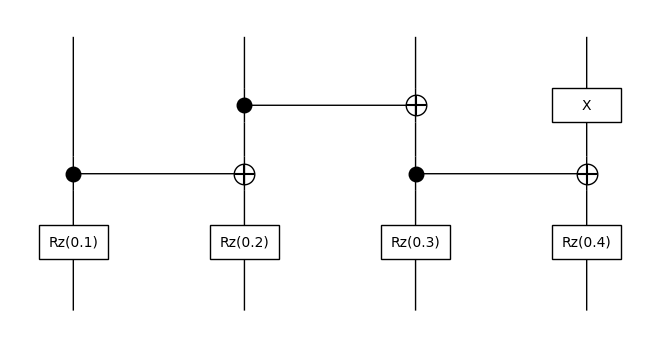
circuit = Id(4)
circuit >>= Id(1) @ CX @ X
circuit >>= CX @ CX
circuit >>= Rz(0.1) @ Rz(0.2) @ Rz(0.3) @ Rz(0.4)
same_circuit = (Id(4).CX(1, 2).X(3).CX(0, 1).CX(2, 3)
.Rz(0.1, 0).Rz(0.2, 1).Rz(0.3, 2).Rz(0.4, 3))
assert circuit == same_circuit
circuit.draw(draw_type_labels=False)
circuit.to_tk()
[12]:
tk.Circuit(4).CX(1, 2).X(3).CX(0, 1).CX(2, 3).Rz(0.2, 0).Rz(0.4, 1).Rz(0.6, 2).Rz(0.8, 3)
To apply multi-qubit gates to non-consecutive qubits, use swaps to permute the wires, apply the gate, then unpermute the wires. These swaps are only logical swaps and do not result in more gates when converted to tket format.
[13]:
from lambeq.backend.quantum import Diagram as Circuit, SWAP
# to apply a CNOT on qubits 2 and 0:
circuit1 = Id(3)
circuit1 >>= SWAP @ Id(1)
circuit1 >>= Id(1) @ SWAP
circuit1 >>= Id(1) @ CX
circuit1 >>= Id(1) @ SWAP
circuit1 >>= SWAP @ Id(1)
# or you can do
perm = Circuit.permutation(circuit1.dom, [2, 0, 1])
circuit2 = perm[::-1] >> Id(1) @ CX >> perm
assert circuit1 == circuit2
circuit1.draw(figsize=(3, 3), draw_type_labels=False)
# no swaps introduced when converting to tket
circuit1.to_tk()
[13]:
tk.Circuit(3).CX(2, 0)
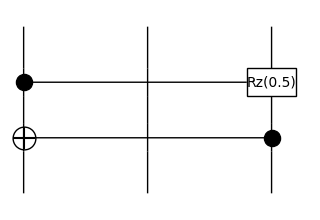
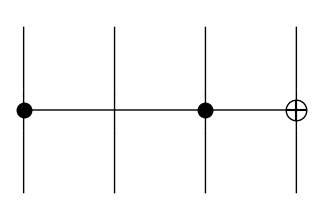
We also have long-ranged controlled gates.
[14]:
from lambeq.backend.quantum import Controlled, Rz, X
(Controlled(Rz(0.5), distance=2) >> Controlled(X, distance=-2)).draw(figsize=(3, 2), draw_type_labels=False)
Controlled(Controlled(X), distance=2).draw(figsize=(3, 2), draw_type_labels=False)
So far, our circuits have been “pure” circuits, consisting of unitaries. Pure circuits can be evaluated locally to return a unitary numpy array. Circuits containing Discards and Measures are considered “mixed”, and return non-unitary numpy arrays when evaluated, as they are classical-quantum maps (for more details, see Chapter 5 in [HV2013]).
[15]:
from lambeq.backend.quantum import Discard, Measure, Ket, Bra
print(f'{Discard().eval()}\n')
print(f'{Measure().eval()}\n')
print(f'{Ket(0).eval()}\n')
# circuits that have measurements in them are no longer unitary
print(f'{(Ket(0) >> Measure()).eval()}\n')
[[1.+0.j 0.+0.j]
[0.+0.j 1.+0.j]]
[[[1.+0.j 0.+0.j]
[0.+0.j 0.+0.j]]
[[0.+0.j 0.+0.j]
[0.+0.j 1.+0.j]]]
[1. 0.]
[1.+0.j 0.+0.j]
Pure circuits can be coerced to evaluate into a classical-quantum map representation by setting mixed=True.
[16]:
CX.eval(mixed=True)
[16]:
array([[[[[[[[1.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 1.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]]],
[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 1.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[1.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]]]],
[[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[1.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 1.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]]],
[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 1.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[1.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]]]]],
[[[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[1.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 1.+0.j],
[0.+0.j, 0.+0.j]]]]],
[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 1.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[1.+0.j, 0.+0.j]]]]]],
[[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[1.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 1.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]]],
[[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[0.+0.j, 1.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]],
[[[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]],
[[[0.+0.j, 0.+0.j],
[1.+0.j, 0.+0.j]],
[[0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j]]]]]]]])
Note that the tensor order of classical-quantum maps is doubled, compared to that of pure quantum circuits:
[17]:
print(CX.eval().shape)
print(CX.eval(mixed=True).shape)
(2, 2, 2, 2)
(2, 2, 2, 2, 2, 2, 2, 2)
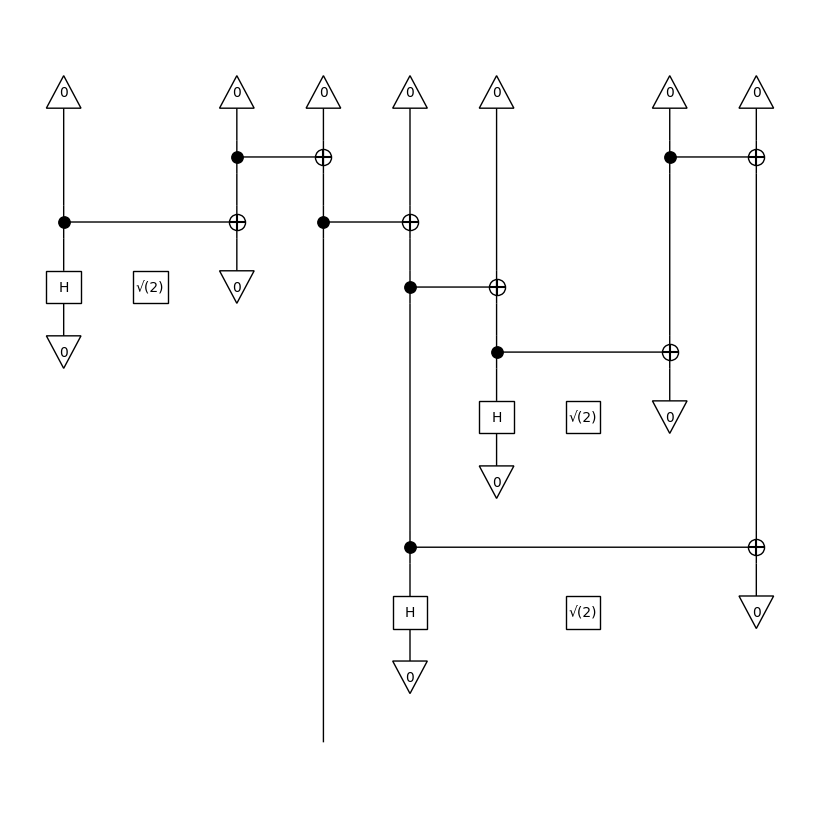
We can implement a functor from string diagrams to quantum circuits like so.
[18]:
from lambeq.backend.grammar import Functor
from lambeq.backend.quantum import quantum, Id
def cnot_ob(_, ty):
# this implicitly maps all rigid types to 1 qubit
return qubit ** len(ty)
def cnot_ar(_, box):
dom = len(box.dom)
cod = len(box.cod)
width = max(dom, cod)
circuit = Id(width)
for i in range(width - 1):
circuit >>= Id(i) @ CX.to_diagram() @ Id(width - i - 2)
# Add Bras (post-selection) and Kets (states)
# to get a circuit with the right amount of
# input and output wires
if cod <= dom:
circuit >>= Id(cod) @ Bra(*[0]*(dom - cod)).to_diagram()
else:
circuit = Id(dom) @ Ket(*[0]*(cod - dom)).to_diagram() >> circuit
return circuit
cnot_functor = Functor(target_category=quantum, ob=cnot_ob, ar=cnot_ar)
diagram.draw(figsize=(5, 2))
cnot_functor(diagram).draw(figsize=(8, 8), draw_type_labels=False)