Step 2. Diagram rewriting
Syntactic derivations in pregroup form can become extremely complicated, which may lead to excessive use of hardware resources and prohibitively long training times. The purpose of the rewrite module is to provide a means to the user to address some of these problems, via rewriters and rewriting rules that simplify the string diagram. lambeq provides two kinds of rewriters:
Box-level rewriters utilize a sequence of functorial transformations on the diagram through rewriting rules. Each rewriting rule independently accesses individual boxes within the diagram, limiting its visibility to information solely within that specific box, without access to the broader diagram context.
Rewriters operating at the diagram-level function procedurally, implementing unrestricted transformations across the entirety of the diagram.
lambeq’s rewriters are explained in detail in the following sections.
Box-level rewrite rules
We will demonstrate the use of box-level rewriting rules using again the sentence “John walks in the park”.
[1]:
from lambeq import BobcatParser
# Parse the sentence
parser = BobcatParser(verbose='suppress')
diagram = parser.sentence2diagram("John walks in the park")
diagram.draw(figsize=(11,5), fontsize=13)
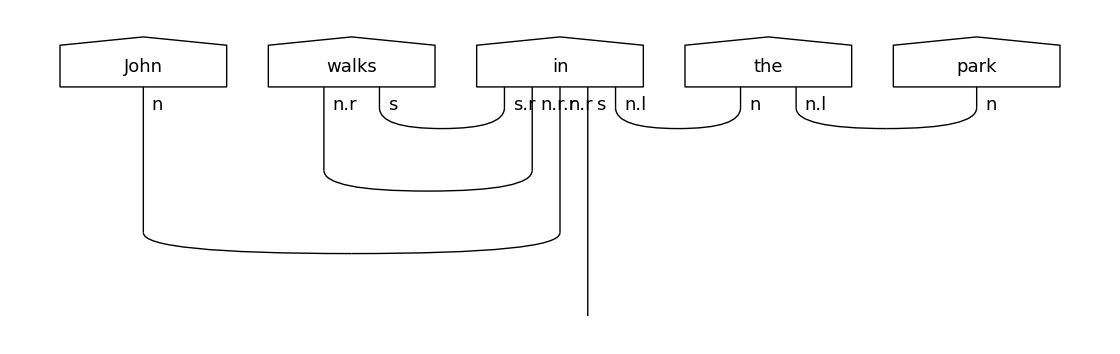
Note that the representation of the preposition is a tensor of order 5 in the “classical” case, or a state of 5 quantum systems in the quantum case. Applying the prepositional_phrase rewriting rule to the diagram takes advantage of the underlying compact-closed monoidal structure, by using a “cap” to bridge the discontinued subject noun wire within the preposition tensor. Furthermore, the determiner rewriting rule will apply a cap on type \(n \cdot n^l\), eliminating completely the determiner “the”.
[2]:
from lambeq import Rewriter
# Apply rewrite rule for prepositional phrases
rewriter = Rewriter(['prepositional_phrase', 'determiner'])
rewritten_diagram = rewriter(diagram)
rewritten_diagram.draw(figsize=(11,5), fontsize=13)

We will now ask lambeq to normalise the diagram, by “stretching” the wires and re-arranging the boxes if required:
[3]:
normalised_diagram = rewritten_diagram.normal_form()
normalised_diagram.draw(figsize=(9,4), fontsize=13)
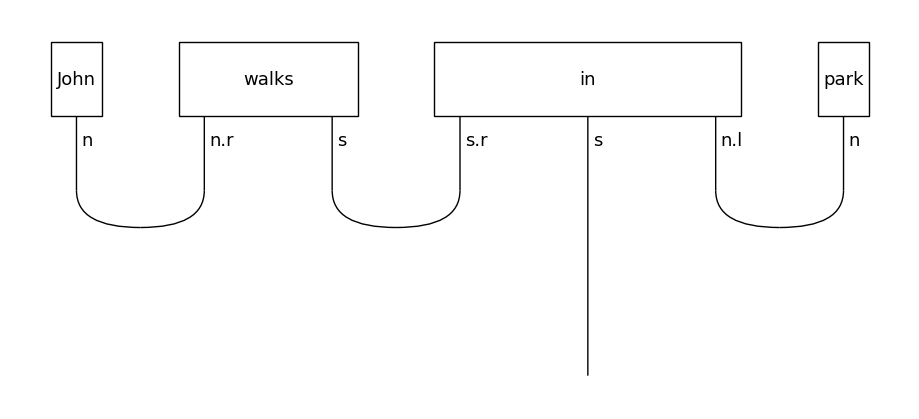
In the simplified diagram, the order of the preposition tensor is reduced by 2, which at least for a classical experiment, is a substantial improvement. Note also that the determiner is now eliminated, equating the meaning of the noun phrase “the park” with that of the noun “park”.
Another very useful rewrite rule is the CurryRewriteRule, which allows us to convert adjoint output wires into input wires using map-state duality. For example:
[4]:
curry_functor = Rewriter(['curry'])
curried_diagram = curry_functor(normalised_diagram)
curried_diagram.draw(figsize=(9,4), fontsize=13)
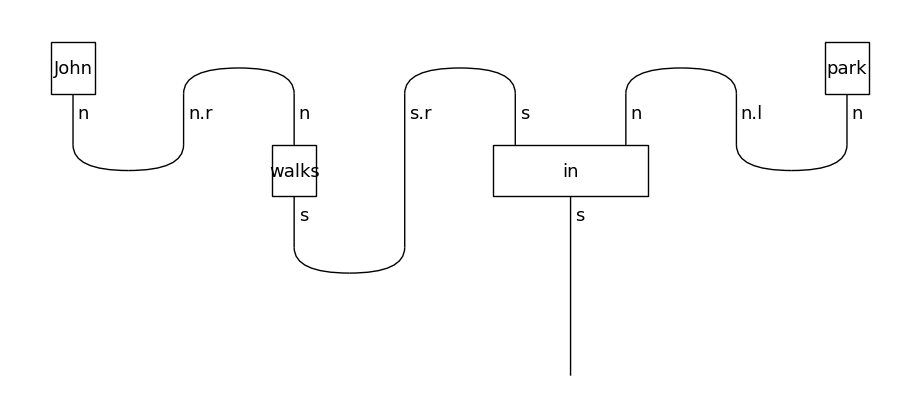
After normalisation the resulting diagram no longer contains any cups, which eliminates post-selection and allows for faster execution.
[5]:
curried_diagram.normal_form().draw(figsize=(5,4), fontsize=13)
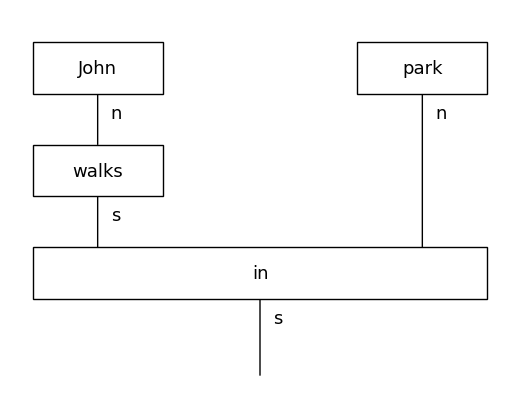
These examples clearly demonstrate the flexibility of string diagrams compared to simple tensor networks, which was one of the main reasons for choosing them as lambeq’s representation format. lambeq comes with a number of standard rewrite rules covering auxiliary verbs, connectors, coordinators, adverbs, determiners, relative pronouns, and prepositional phrases.
Rewrite rule |
Description |
|---|---|
|
Removes auxiliary verbs (such as “do”) by replacing them with caps. |
|
Removes sentence connectors (such as “that”) by replacing them with caps. |
|
Simplifies “and” by replacing it with a layer of interleaving spiders. |
|
Uses map-state duality to reduce the number of cups in the diagram. |
|
Removes determiners (such as “the”) by replacing them with caps. |
|
Simplifies relative pronouns (such as “that”) using cups, spiders and a loop. |
|
Simplifies adverbs by passing through the noun wire transparently using a cap. |
|
Simplifies prepositions by passing through the noun wire using a cap. |
Diagram-level rewriters
While box-level rewriters and rewrite rules access one box at a time, for certain cases of more general transformations you will require knowledge of the broader context in the diagram. For example, imagine the following derivation:
[6]:
from lambeq.backend.grammar import Diagram, Word, Ty, Cup
from lambeq import AtomicType
n = AtomicType.NOUN
s = AtomicType.SENTENCE
words = [Word('do', n.r @ s @ n.l), Word('your', n @ n.l),
Word('homework', n), Word('now', s.r @ s)]
morphisms = [(Cup, 2, 3), (Cup, 4, 5), (Cup, 1, 6)]
diagram = Diagram.create_pregroup_diagram(words, morphisms)
diagram.draw(figsize=(5,2))
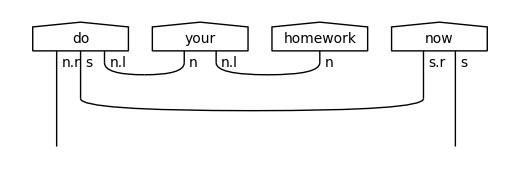
Note that this diagram has two free wires, coming from different boxes. In cases like these, if your loss function expects a single wire, you are going to get a dimension mismatch error. The probem can be addressed by merging the two free wires into one, so you are able to train your model in a consistent way. In lambeq, this can be done with the UnifyCodomainRewriter, which acts at the diagram level. Specifically, the rewriter looks at the codomain of the diagram (in the above case \(n^r \cdot s\)), and if this consists of more than one wires, it merges these wires with an extra box.
[7]:
from lambeq import UnifyCodomainRewriter
rewriter = UnifyCodomainRewriter(output_type=s)
rewriter(diagram).draw(figsize=(5,4))
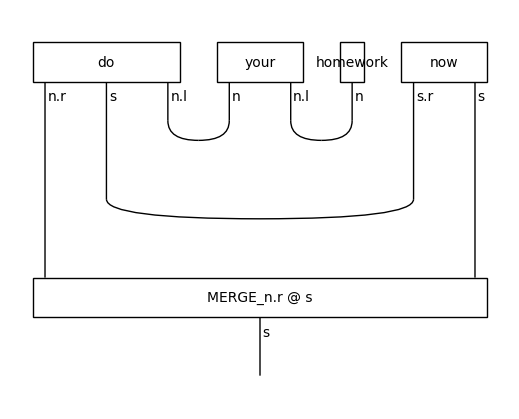
This type of transformation would not be possible with box-level rewriters, since it requires knowledge that is available in more than one boxes.
Other diagram-level rewriters that are available in lambeq:
RemoveCupsRewriter: Removes the cups from a diagram, reducing or eliminating post-selection.RemoveSwapsRewriter: Removes the swaps from a diagram, producing a proper pregroup diagram, following J. Lambek’s definition.
More diagram-level rewriters can be created by extending the class DiagramRewriter.
See also: