Step 3. Parameterisation

Up to this point of the pipeline, a sentence is still represented as a string diagram, independent of any low-level decisions such as tensor dimensions or specific quantum gate choices. This abstract form can be turned into a concrete quantum circuit or tensor network by applying ansätze. An ansatz can be seen as a map that determines choices such as the number of qubits that every wire of the string diagram is associated with and the concrete parameterised quantum states that correspond to each word. In lambeq, ansätze can be added by extending one of the classes TensorAnsatz or CircuitAnsatz depending on the type of the experiment.

Download code

Quantum case

For the quantum case, the library comes equipped with the following ansätze:

Ansatz	Description
IQPAnsatz	Instantaneous Quantum Polynomial ansatz. An IQP ansatz interleaves layers of Hadamard gates with diagonal unitaries. This class uses n_layers-1 adjacent CRz gates to implement each diagonal unitary (see [Hea2019])
Sim14Ansatz	A modification of Circuit 14 from [SJA2019]. Replaces circuit-block construction with two rings of CRx gates, in opposite orientation.
Sim15Ansatz	A modification of Circuit 15 from [SJA2019]. Replaces circuit-block construction with two rings of CNOT gates, in opposite orientation.
Sim4Ansatz	Circuit 4 from [SJA2019]. Uses a layer each of Rx and Rz gates, followed by a ladder of CRx gates per layer.
StronglyEntanglingAnsatz	Ansatz using three single qubit rotations (RzRyRz) followed by a ladder of CNOT gates with different ranges per layer. Adapted from the PennyLane implementation of StronglyEntanglingLayers.

In the example below we will use the class IQPAnsatz, which turns the string diagram into a standard IQP circuit.

from lambeq import BobcatParser

sentence = 'John walks in the park'

# Get a string diagram
parser = BobcatParser(verbose='text')
diagram = parser.sentence2diagram(sentence)

In order to create an IQPAnsatz instance, we need to define the number of qubits for all atomic types that occur in the diagram – in this case, for the noun type and the sentence type. The following code produces a circuit by assigning 1 qubit to the noun type and 1 qubit to the sentence type. Further, the number of IQP layers (n_layers) is set to 2.

from lambeq import AtomicType, IQPAnsatz

# Define atomic types
N = AtomicType.NOUN
S = AtomicType.SENTENCE

# Convert string diagram to quantum circuit
ansatz = IQPAnsatz({N: 1, S: 1}, n_layers=2)
circuit = ansatz(diagram)
circuit.draw(figsize=(15,10))

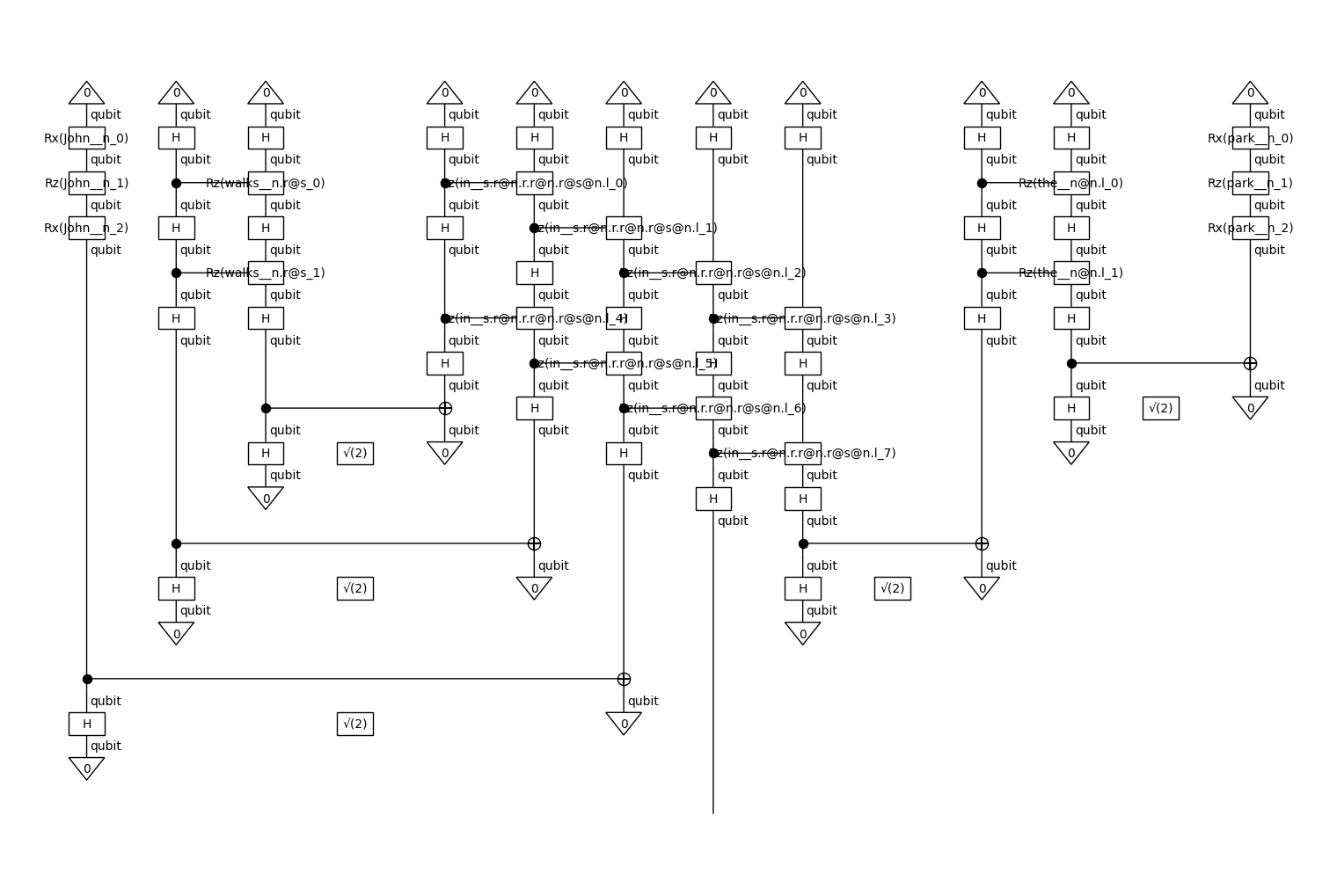
This produces a quantum circuit in lambeq.backend.quantum.Diagram form.

Note

Lambeq also includes other circuit ansätze. See CircuitAnsatz for further reference.

Conversion to pytket format is very simple:

from pytket.circuit.display import render_circuit_jupyter

tket_circuit = circuit.to_tk()

render_circuit_jupyter(tket_circuit)

Exporting to pytket format provides additional functionality and allows interoperability. For example, obtaining a Qiskit circuit is trivial:

from pytket.extensions.qiskit import tk_to_qiskit

qiskit_circuit = tk_to_qiskit(tket_circuit)

Note

To use tk_to_qiskit, first install the pytket-qiskit extension by running pip install pytket-qiskit. For more information see the pytket documentation.

Classical case

In the case of a classical experiment, instantiating one of the tensor ansätze requires the user to assign dimensions to each one of the atomic types occurring in the diagram. In the following code, we parameterise a TensorAnsatz instance with \(d_n=4\) for the base dimension of the noun space, and \(d_s=2\) as the dimension of the sentence space:

from lambeq import TensorAnsatz
from lambeq.backend.tensor import Dim

tensor_ansatz = TensorAnsatz({N: Dim(4), S: Dim(2)})
tensor_diagram = tensor_ansatz(diagram)

tensor_diagram.draw(figsize=(10,4), fontsize=13)

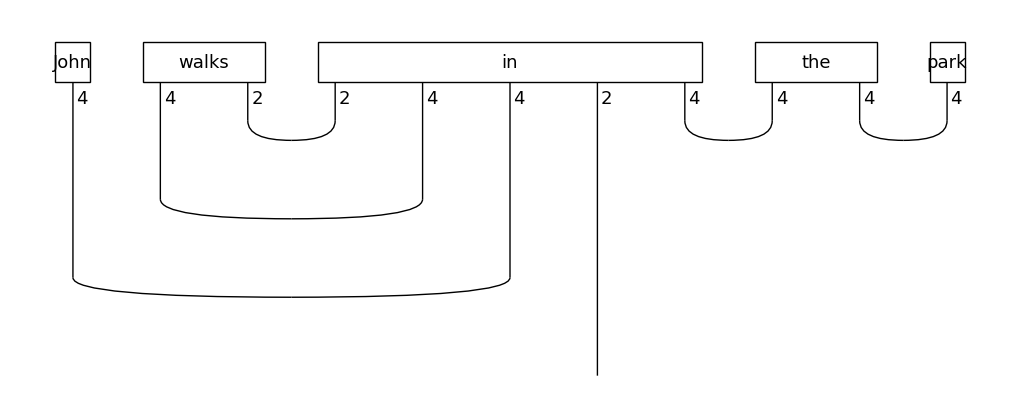
Note that the wires of the diagram are now annotated with the dimensions corresponding to each type, indicating that the result is a concrete tensor network.

Matrix product states

In classical experiments of this kind, the tensors associated with certain words, such as conjunctions, can become extremely large. In some cases, the order of these tensors can be 12 or even higher (\(d^{12}\) elements, where \(d\) is the base dimension), which makes efficient execution of the experiment impossible. In order to address this problem, lambeq includes ansätze for converting tensors into various forms of matrix product states (MPSs).

The following code applies the SpiderAnsatz, which splits tensors with order greater than 2 to sequences of order-2 tensors (i.e. matrices), connected with spiders.

from lambeq import SpiderAnsatz
from lambeq.backend.tensor import Dim

spider_ansatz = SpiderAnsatz({N: Dim(4), S: Dim(2)})
spider_diagram = spider_ansatz(diagram)
spider_diagram.draw(figsize=(13,6), fontsize=13)

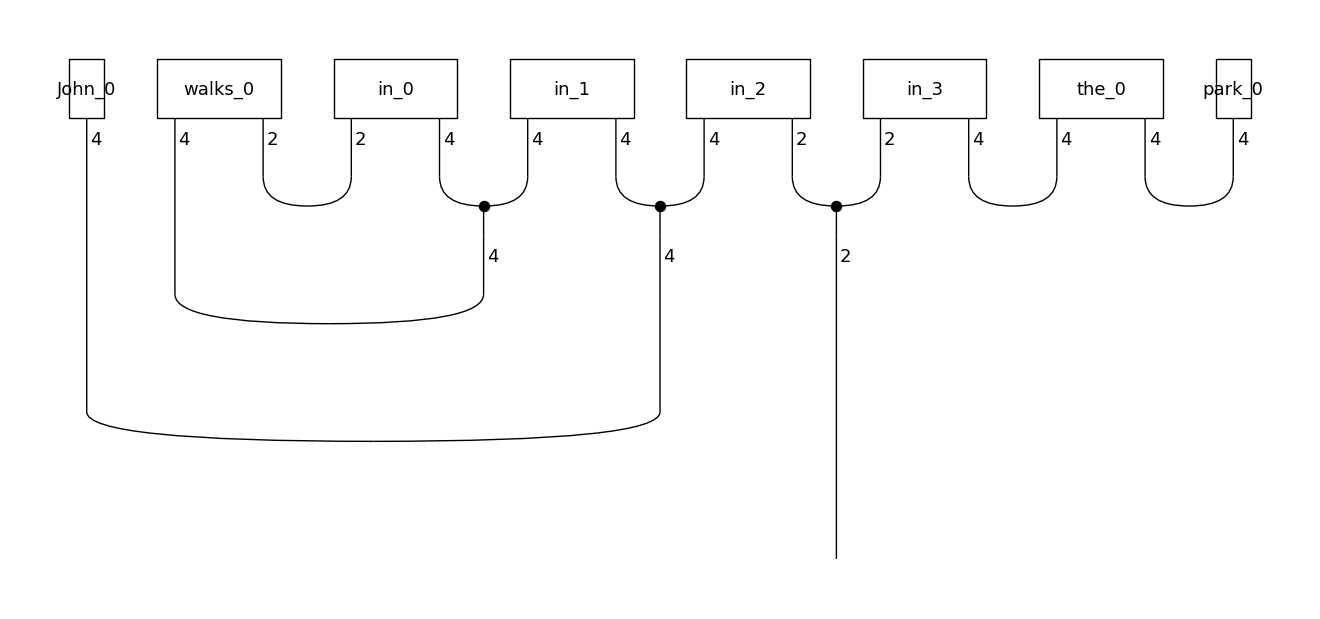
Note that the preposition “in” is now represented by a matrix product state of 4 linked matrices, which is a very substantial reduction in the space required to store the tensors.

Another option is the MPSAnsatz class, which converts large tensors to sequences of order-3 tensors connected with cups. In this setting, the user needs to also define the bond dimension, that is, the dimensionality of the wire that connects the tensors together.

from lambeq import MPSAnsatz
from lambeq.backend.tensor import Dim

mps_ansatz = MPSAnsatz({N: Dim(4), S: Dim(2)}, bond_dim=3)
mps_diagram = mps_ansatz(diagram)
mps_diagram.draw(figsize=(13,7), fontsize=13)

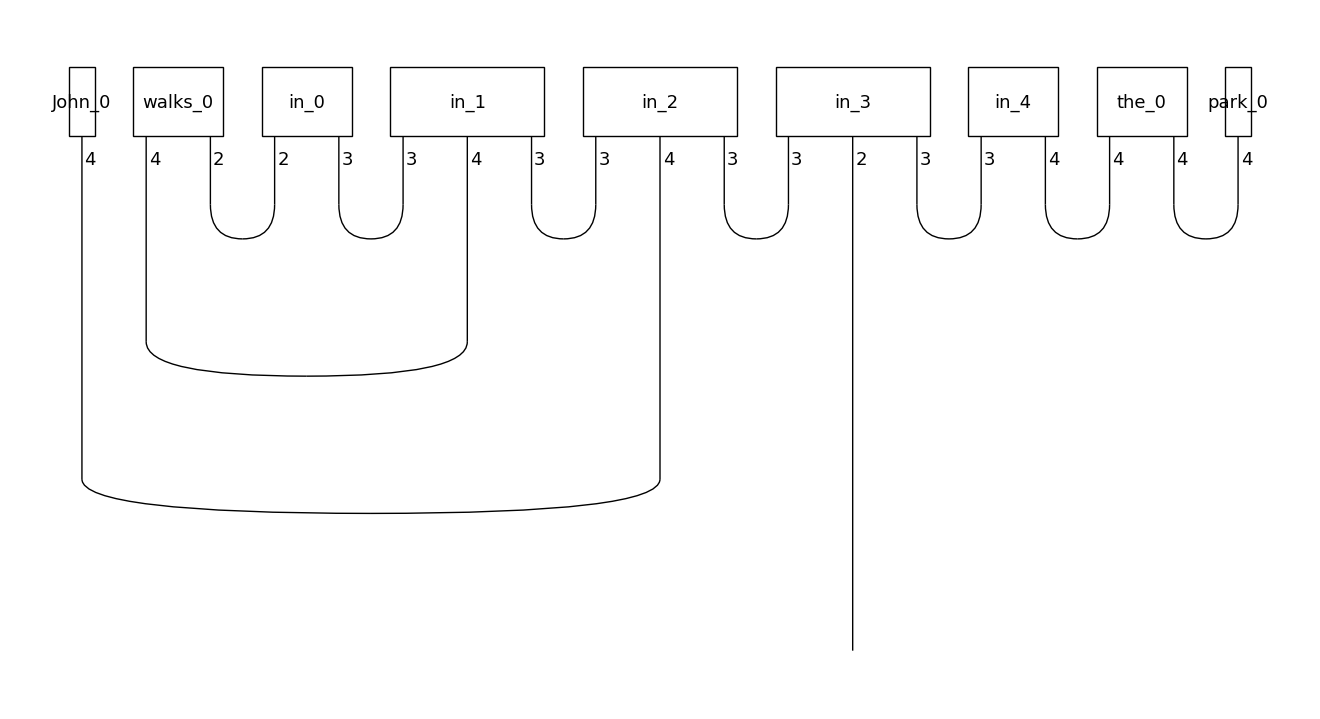
See also:

• lambeq.ansatz package

• Example notebook tensor.ipynb

• Example notebook circuit.ipynb

• DisCoCat in lambeq

• Extending lambeq