Introduction to symbols

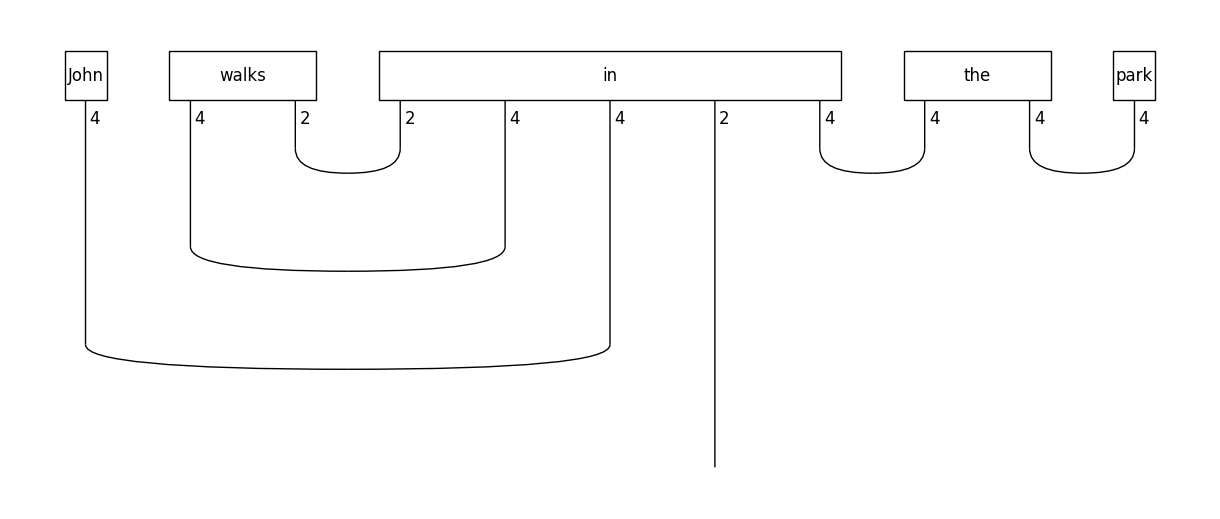
The parameterisable parts of a diagram are represented by symbols; these are instances of the lambeq.Symbol class. Let’s create a tensor diagram for a sentence:

Download code

import warnings
warnings.filterwarnings('ignore')

from lambeq import AtomicType, BobcatParser, TensorAnsatz
from lambeq.backend.tensor import Dim

# Define atomic types
N = AtomicType.NOUN
S = AtomicType.SENTENCE

# Parse a sentence
parser = BobcatParser(verbose='suppress')
diagram = parser.sentence2diagram('John walks in the park')

# Apply a tensor ansatz
ansatz = TensorAnsatz({N: Dim(4), S: Dim(2)})
tensor_diagram = ansatz(diagram)
tensor_diagram.draw(figsize=(12,5), fontsize=12)

Note

Class Symbol inherits from class sympy.Symbol.

The symbols of the diagram can be accessed by the free_symbols attribute:

tensor_diagram.free_symbols

{John__n, in__s.r@n.r.r@n.r@s@n.l, park__n, the__n@n.l, walks__n.r@s}

Each symbol is associated with a specific size, which is defined from the applied ansatz.

[(s, s.size) for s in tensor_diagram.free_symbols]

[(in__s.r@n.r.r@n.r@s@n.l, 256),
 (walks__n.r@s, 8),
 (John__n, 4),
 (the__n@n.l, 16),
 (park__n, 4)]

For example, you see that preposition “in” has been assigned 256 dimensions, which is derived by multiplying the dimensions of each individual wire (\(2 \cdot 4 \cdot 4 \cdot 2 \cdot 4\)), nouns are assigned 4 dimensions, and the determiner 16 dimensions.

Circuit symbols

We will now convert the original diagram into a quantum circuit and examine its parameters:

from lambeq import IQPAnsatz

iqp_ansatz = IQPAnsatz({N: 1, S: 1}, n_layers=1)
circuit = iqp_ansatz(diagram)
circuit.draw(figsize=(12,8), fontsize=12)

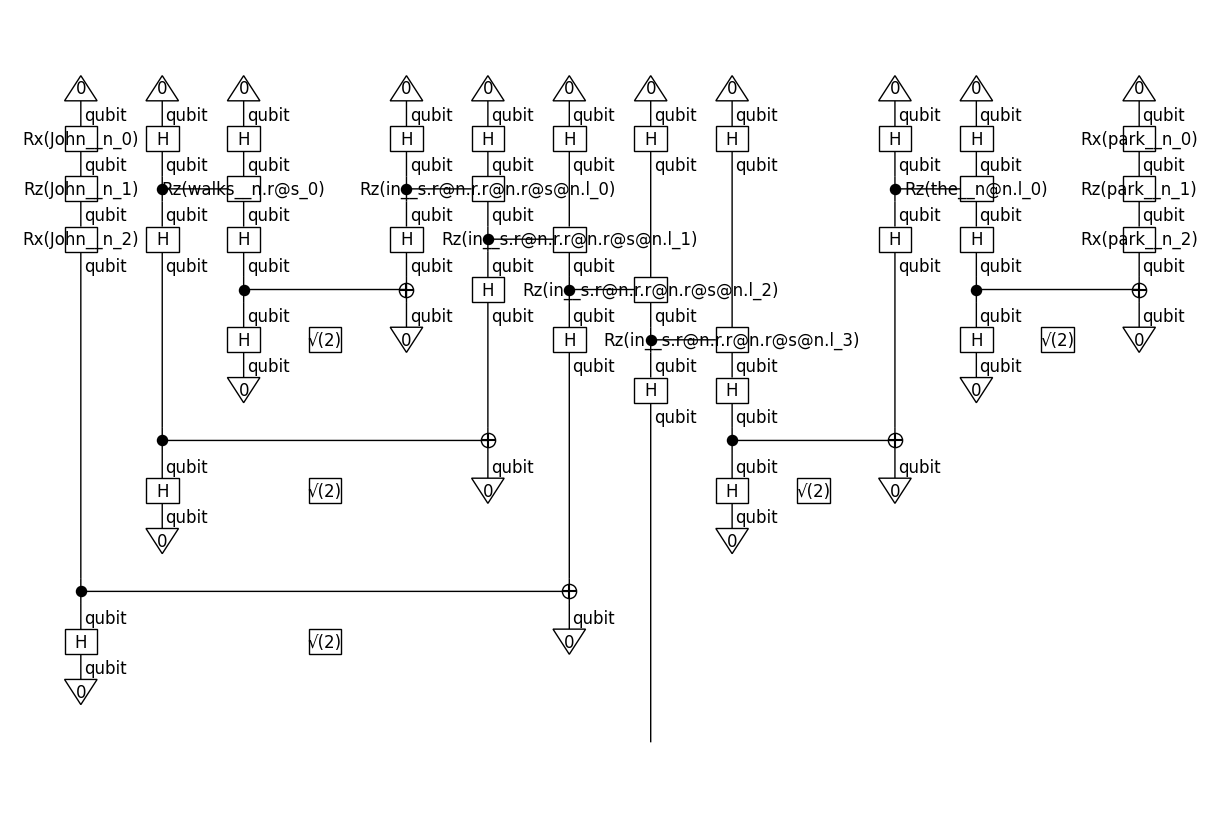
Let’s see the symbols of the circuit:

circuit.free_symbols

{John__n_0,
 John__n_1,
 John__n_2,
 in__s.r@n.r.r@n.r@s@n.l_0,
 in__s.r@n.r.r@n.r@s@n.l_1,
 in__s.r@n.r.r@n.r@s@n.l_2,
 in__s.r@n.r.r@n.r@s@n.l_3,
 park__n_0,
 park__n_1,
 park__n_2,
 the__n@n.l_0,
 walks__n.r@s_0}

In contrast to the tensor case, the above symbols are not associated with a specific size; this is because the parameters of the circuit are not tensors but numbers (i.e. “tensors” of size 1), defining rotation angles on qubits.

From symbols to tensors

In this section we will create actual tensors and associate them with the symbols of the diagram. In order to do this, we first need to fix the order of the symbols, since they are represented as a set. We can use sympy’s default_sort_key for this purpose.

from sympy import default_sort_key

parameters = sorted(tensor_diagram.free_symbols, key=default_sort_key)

We will use numpy arrays for the tensors, initialised randomly:

import numpy as np

tensors = [np.random.rand(p.size) for p in parameters]
print(tensors[0])

[0.20328544 0.6856217  0.6337871  0.57768928]

Associating the numpy arrays with the symbols in the diagram can be done by using the lambdify() method:

tensor_diagram_np = tensor_diagram.lambdify(*parameters)(*tensors)
print("Before lambdify:", tensor_diagram.boxes[0].data)
print("After lambdify:", tensor_diagram_np.boxes[0].data)

Before lambdify: John__n
After lambdify: [0.20328544 0.6856217  0.6337871  0.57768928]

To contract the tensor network and compute a representation for the sentence, we will use eval().

result = tensor_diagram_np.eval(dtype=float)
print(result)

[18.41306384 16.09003165]

Note

The result is a 2-dimensional array, based on the fact that we have assigned a dimension of 2 to the sentence space when applying the ansatz.

The result is an instance of the numpy.ndarray class.

result

array([18.41306384, 16.09003165])