Training: Quantum case

In this tutorial we will train a lambeq model to solve the relative pronoun classification task presented in [Lea2021]. The goal is to predict whether a noun phrase contains a subject-based or an object-based relative clause. The entries of this dataset are extracted from the RelPron dataset [Rea2016].

We will use an IQPAnsatz to convert string diagrams into quantum circuits. The pipeline uses tket as a backend.

If you have already gone through the classical training tutorial, you will see that there are only minor differences for the quantum case.

Download code

Preparation

We start with importing NumPy and specifying some training hyperparameters.

import os
import warnings

warnings.filterwarnings('ignore')
os.environ['TOKENIZERS_PARALLELISM'] = 'true'

Note

We disable warnings to filter out issues with the tqdm package used in jupyter notebooks. Furthermore, we have to specify whether we want to use parallel computation for the tokenizer used by the BobcatParser. None of the above impairs the performance of the code.

import numpy as np

BATCH_SIZE = 10
EPOCHS = 100
SEED = 2

Input data

Let’s read the data and print some example sentences.

def read_data(filename):
    labels, sentences = [], []
    with open(filename) as f:
        for line in f:
            t = int(line[0])
            labels.append([t, 1-t])
            sentences.append(line[1:].strip())
    return labels, sentences


train_labels, train_data = read_data('../examples/datasets/rp_train_data.txt')
val_labels, val_data = read_data('../examples/datasets/rp_test_data.txt')

train_data[:5]

['organization that church establish .',
 'organization that team join .',
 'organization that company sell .',
 'organization that soldier serve .',
 'organization that sailor join .']

Targets are represented as 2-dimensional arrays:

train_labels[:5]

[[1, 0], [1, 0], [1, 0], [1, 0], [1, 0]]

Creating and parameterising diagrams

The first step is to convert sentences into string diagrams.

Note

We know that the specific dataset only consists of noun phrases, hence, we reduce potential parsing errors by restricting the parser to only return parse trees with the root categories N (noun) and NP (noun phrase).

from lambeq import BobcatParser

parser = BobcatParser(root_cats=('NP', 'N'), verbose='text')

raw_train_diagrams = parser.sentences2diagrams(train_data, suppress_exceptions=True)
raw_val_diagrams = parser.sentences2diagrams(val_data, suppress_exceptions=True)

Tagging sentences.
Parsing tagged sentences.
Turning parse trees to diagrams.
Tagging sentences.
Parsing tagged sentences.
Turning parse trees to diagrams.

Filter and simplify diagrams

We simplify the diagrams by calling normal_form() and filter out any diagrams that could not be parsed.

train_diagrams = [
    diagram.normal_form()
    for diagram in raw_train_diagrams if diagram is not None
]
val_diagrams = [
    diagram.normal_form()
    for diagram in raw_val_diagrams if diagram is not None
]

train_labels = [
    label for (diagram, label)
    in zip(raw_train_diagrams, train_labels)
    if diagram is not None]
val_labels = [
    label for (diagram, label)
    in zip(raw_val_diagrams, val_labels)
    if diagram is not None
]

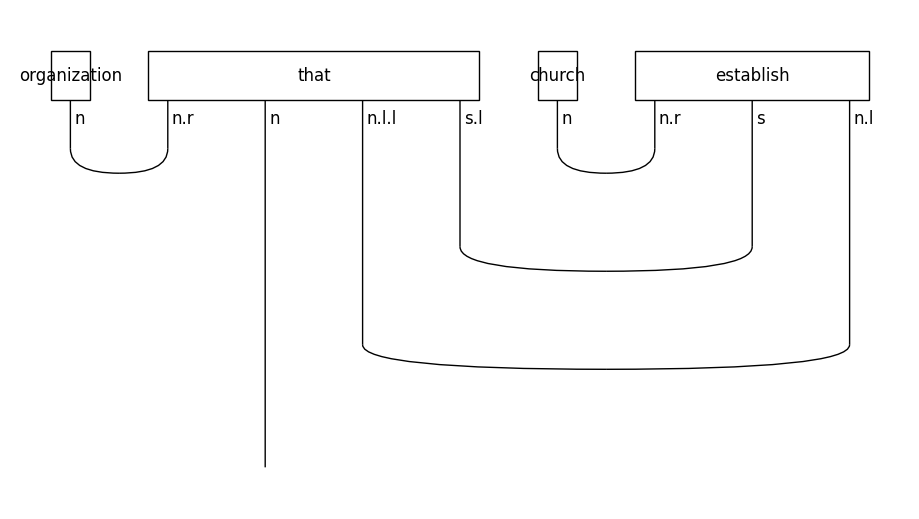
Let’s see the form of the diagram for a relative clause on the subject of a sentence:

train_diagrams[0].draw(figsize=(9, 5), fontsize=12)

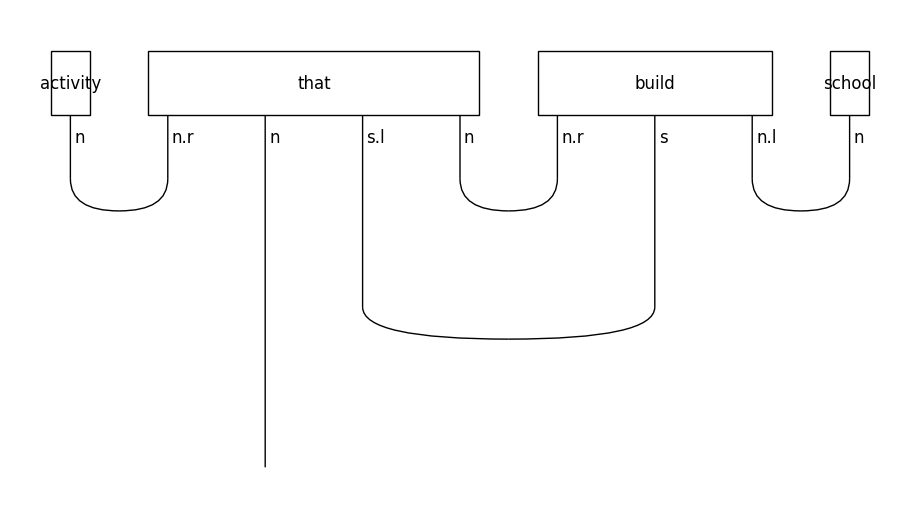
In object-based relative clauses the noun that follows the relative pronoun is the object of the sentence:

train_diagrams[-1].draw(figsize=(9, 5), fontsize=12)

Create circuits

In order to run the experiments on a quantum computer, we need to apply to string diagrams a quantum ansatz. For this experiment, we will use an IQPAnsatz, where noun wires (n) are represented by a one-qubit system, and sentence wires (s) are discarded (since we deal with noun phrases).

from lambeq import AtomicType, IQPAnsatz, RemoveCupsRewriter

ansatz = IQPAnsatz({AtomicType.NOUN: 1, AtomicType.SENTENCE: 0},
                   n_layers=1, n_single_qubit_params=3)
remove_cups = RemoveCupsRewriter()

train_circuits = [ansatz(remove_cups(diagram)) for diagram in train_diagrams]
val_circuits =  [ansatz(remove_cups(diagram))  for diagram in val_diagrams]

train_circuits[0].draw(figsize=(9, 10))

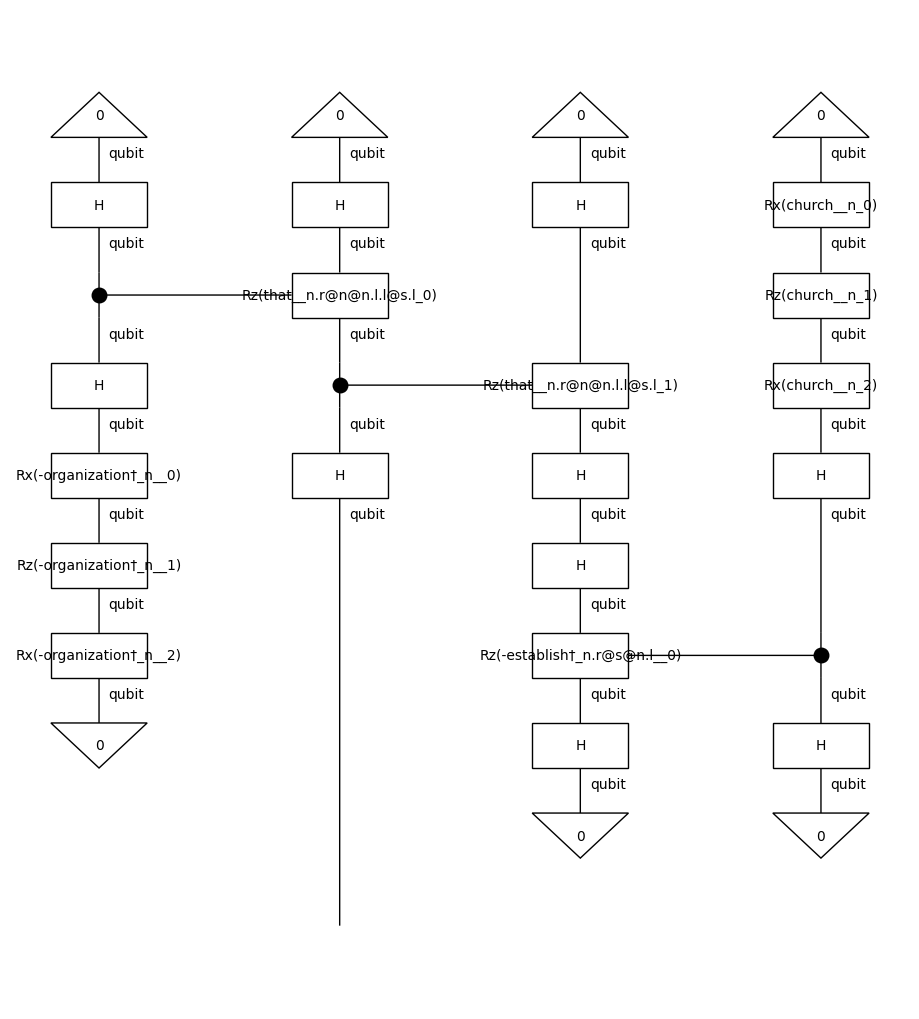
Note that we remove the cups before parameterising the diagrams. By doing so, we reduce the number of post-selections, which makes the model computationally more efficient. The effect of cups removal on a string diagram is demonstrated below:

from lambeq.backend import draw_equation

original_diagram = train_diagrams[0]
removed_cups_diagram = remove_cups(original_diagram)

draw_equation(original_diagram, removed_cups_diagram, symbol='-->', figsize=(9, 6), asymmetry=0.3, fontsize=12)

Training

Instantiate the model

We will use a TketModel, which we initialise by passing all diagrams to the class method TketModel.from_diagrams(). The TketModel needs a backend configuration dictionary passed as a keyword argument to the initialisation method. This dictionary must contain entries for backend, compilation and shots. The backend is provided by pytket-extensions. In this example, we use Qiskit‘s AerBackend with 8192 shots.

from pytket.extensions.qiskit import AerBackend
from lambeq import TketModel

all_circuits = train_circuits + val_circuits

backend = AerBackend()
backend_config = {
    'backend': backend,
    'compilation': backend.default_compilation_pass(2),
    'shots': 8192
}

model = TketModel.from_diagrams(all_circuits, backend_config=backend_config)

Note

The model can also be instantiated by calling TketModel.from_checkpoint(), in case a pre-trained checkpoint is available.

Define loss and evaluation metric

We use standard binary cross-entropy as the loss. Optionally, we can provide a dictionary of callable evaluation metrics with the signature metric(y_hat, y).

from lambeq import BinaryCrossEntropyLoss

# Using the builtin binary cross-entropy error from lambeq
bce = BinaryCrossEntropyLoss()

acc = lambda y_hat, y: np.sum(np.round(y_hat) == y) / len(y) / 2  # half due to double-counting
eval_metrics = {"acc": acc}

Initialise trainer

In lambeq, quantum pipelines are based on the QuantumTrainer class. Furthermore, we will use the standard lambeq SPSA optimizer, implemented in the SPSAOptimizer class. This needs three hyperameters:

• a: The initial learning rate (decays over time),

• c: The initial parameter shift scaling factor (decays over time),

• A: A stability constant, best choice is approx. 0.01 * number of training steps.

from lambeq import QuantumTrainer, SPSAOptimizer

trainer = QuantumTrainer(
    model,
    loss_function=bce,
    epochs=EPOCHS,
    optimizer=SPSAOptimizer,
    optim_hyperparams={'a': 0.05, 'c': 0.06, 'A':0.001*EPOCHS},
    evaluate_functions=eval_metrics,
    evaluate_on_train=True,
    verbose = 'text',
    log_dir='RelPron/logs',
    seed=0
)

Create datasets

To facilitate data shuffling and batching, lambeq provides a native Dataset class. Shuffling is enabled by default, and if not specified, the batch size is set to the length of the dataset.

from lambeq import Dataset

train_dataset = Dataset(
            train_circuits,
            train_labels,
            batch_size=BATCH_SIZE)

val_dataset = Dataset(val_circuits, val_labels, shuffle=False)

Train

We can now pass the datasets to the fit() method of the trainer to start the training. Here, we perform early stopping if the validation accuracy doesn’t improve within the specified early_stopping_interval epochs.

trainer.fit(train_dataset, val_dataset,
            early_stopping_criterion='acc',
            early_stopping_interval=5,
            minimize_criterion=False)

Epoch 1:    train/loss: 0.5620   valid/loss: 2.4878   train/acc: 0.6214   valid/acc: 0.6613
Epoch 2:    train/loss: 0.7484   valid/loss: 2.3023   train/acc: 0.4786   valid/acc: 0.4355
Epoch 3:    train/loss: 0.5687   valid/loss: 2.1669   train/acc: 0.5714   valid/acc: 0.4839
Epoch 4:    train/loss: 0.5116   valid/loss: 1.7920   train/acc: 0.6071   valid/acc: 0.6935
Epoch 5:    train/loss: 2.6042   valid/loss: 1.9361   train/acc: 0.7286   valid/acc: 0.7742
Epoch 6:    train/loss: 0.6296   valid/loss: 1.4529   train/acc: 0.6000   valid/acc: 0.5000
Epoch 7:    train/loss: 0.5425   valid/loss: 1.4265   train/acc: 0.5643   valid/acc: 0.5806
Epoch 8:    train/loss: 2.1077   valid/loss: 2.3139   train/acc: 0.5000   valid/acc: 0.3871
Epoch 9:    train/loss: 0.2571   valid/loss: 2.4732   train/acc: 0.6643   valid/acc: 0.6129
Epoch 10:   train/loss: 1.7144   valid/loss: 2.9791   train/acc: 0.6929   valid/acc: 0.5000
Early stopping!
Best model (epoch=5, step=35) saved to
RelPron/logs/best_model.lt

Training completed!

Results

Finally, we visualise the results and evaluate the model on the test data.

import matplotlib.pyplot as plt

fig, ((ax_tl, ax_tr), (ax_bl, ax_br)) = plt.subplots(2, 2, sharex=True, sharey='row', figsize=(10, 6))
ax_tl.set_title('Training set')
ax_tr.set_title('Development set')
ax_bl.set_xlabel('Epochs')
ax_br.set_xlabel('Epochs')
ax_bl.set_ylabel('Accuracy')
ax_tl.set_ylabel('Loss')

colours = iter(plt.rcParams['axes.prop_cycle'].by_key()['color'])
range_ = np.arange(1, len(trainer.train_epoch_costs)+1)
ax_tl.plot(range_, trainer.train_epoch_costs, color=next(colours))
ax_bl.plot(range_, trainer.train_eval_results['acc'], color=next(colours))
ax_tr.plot(range_, trainer.val_costs, color=next(colours))
ax_br.plot(range_, trainer.val_eval_results['acc'], color=next(colours))

# mark best model as circle
best_epoch = np.argmax(trainer.val_eval_results['acc'])
ax_tl.plot(best_epoch + 1, trainer.train_epoch_costs[best_epoch], 'o', color='black', fillstyle='none')
ax_tr.plot(best_epoch + 1, trainer.val_costs[best_epoch], 'o', color='black', fillstyle='none')
ax_bl.plot(best_epoch + 1, trainer.train_eval_results['acc'][best_epoch], 'o', color='black', fillstyle='none')
ax_br.plot(best_epoch + 1, trainer.val_eval_results['acc'][best_epoch], 'o', color='black', fillstyle='none')

ax_br.text(best_epoch + 1.4, trainer.val_eval_results['acc'][best_epoch], 'early stopping', va='center')

# print test accuracy
model.load(trainer.log_dir + '/best_model.lt')
val_acc = acc(model(val_circuits), val_labels)
print('Validation accuracy:', val_acc.item())

Validation accuracy: 0.7419354838709677

See also:

• Training: Classical case

• Training: Hybrid case

• Advanced: Manual training